Śledztwem kieruje Major BJAB. Kto sprawy nie zna, musi przeczytać kilka poprzednich notek. Ja nadzoruję wykonywanie czynności operacyjnych. Sprawa kręgów nie jest nowa. Już w Makbecie Szekspira (podobno) wspomniano:
Dalej,dalej,siostry wiedźmy,
Czarodziejski krąg zawiedźmy
W naszym przypadku mamy nie jeden krąg, mamy ich nieskończenie wiele. W poprzedniej notce Niebieskie kwaterniony i zemsta Gargamela mamy zdanie:
Teraz tworzymy W(t),X(t),Y(t),Z(t). I z tego bierzemy rzut stereograficzny
x(t) = X(t)/(1-W(t)), y(t) = Y(t)/(1-W(t)), z(t) = Z(t)/(1-W(t))
I to jest punktem wyjścia dla śledztwa. Przede wszystkim formuły jakie otrzymujemy (wynik obliczeń według recepty tam podanej)
x(t) = 2 (x cos(t) + y sin(t)) / mianownik
y(t) = 2 (y cos(t) - x sin(t)) / mianownik
z(t) = (2 z cos(t) + (-1 + x2 + y2 + z2 ) sin(t)) / mianownik
gdzie
mianownik = 1 + x2 + y2 + z2 - (-1 + x2 + y2 + z2) cos(t) + 2 z sin(t)
Są to krzywe przechodzące, dla t=0, przez punkt (x,y,z). A co to za krzywe – to jest właśnie przedmiotem śledztwa.
Śledztwo należałoby rozpocząć od przesłuchania mianownika. Czy czasem się nie zerował, a jak się zerował, to kiedy i z kim? Jednak mianownik jest wredny i ma wysokie chody. Zatem odpuścimy ten etap śledztwa, może w końcu sprawę uda się doprowadzić do końca bez tego.
Przypomnijmy na czym skończyliśmy etap wstępny w notce W otoczeniu Azraela
Śledztwo interesuje się otoczeniem punktu x=y=z=0. W punkcie tym nasze pole ma wartość
V3P(0,0,0) = (0,0,-1/2)
Czyli strzałeczka skierowana w dół. Chcemy teraz przeprowadzić wizję lokalną i zobaczyć co znajdziemy w okolicach tego punktu. No to wybieramy do badania mały kawałek płaszczyzny z=0, Na przykład x,y zmieniają się od -1, do 1, zaś z=0.
Nie zarzucajmy przedwcześnie tej linii śledztwa. Zbadajmy najpierw krzywe przechodzące przez płaszczyznę z=0. Jeśli będziemy mieli szczęście (A czemuż byśmy szczęścia mieć nie mieli? Czy nie zasługujemy na nie?), to okaże się, że wszystkie krzywe tę płaszczyznę przecinają. Zatem w naszych formułach kładziemy z=0. Otrzymujemy
x(t) = 2 (x cos(t) + y sin(t)) / mianownik
y(t) = 2 (y cos(t) - x sin(t)) / mianownik
z(t) = (-1 + x2 + y2) sin(t)) / mianownik
gdzie
mianownik = 1 + x2 + y2 - (-1 + x2 + y2) cos(t)
Widać, że warto wprowadzić zmienne biegunowe r,φ
x = r cos(φ)
y = r sin(φ)
Wtedy
x(t) = 2r (cos(φ) cos(t) + sin(φ) sin(t)) / mianownik
y(t) = 2r (sin(φ) cos(t) - cos(φ) sin(t)) / mianownik
z(t) = (-1+ r2) sin(t)) / mianownik
mianownik = 1 + r2 + (1 - r2) cos(t)
Ze względu na delikatność sprawy, dalsza część dochodzenia musi pozostać utajniona. Można jednak podać ostateczne wyniki. Oto wyniki, które otrzymuje prowadzący śledztwo.
- Wszystkie te krzywe to okręgi o skończonych promieniach. Wyjątkiem jest prosta, okrąg o nieskończonym promieniu, dla r=0. Jest to po prostu oś z.
- Środek każdego z tych okręgów leży w płaszczyźnie z = 0.
- Jeden okrąg leży całkowicie w płaszczyźnie z=0. Jest to okrąg r=1.
- Każdy inny okrąg przecina płaszczyznę z=0 w dwóch punktach. Jednym w odległości r od zera, drugim w odległości 1/r od zera. Badając te okręgi wystarczy zatem zbadać te przechodzące przez punkty z r<1.
Okrąg przechodzący przez punkt r, φ ma środek w punkcie x0,y0 i promień r0 dane przez poniższe formuły (w kodzie Mathematica)
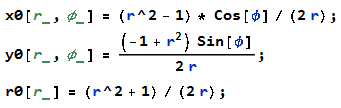
Okrąg przechodzący przez punkt r, φ leży w płaszczyźnie prostopadłej do wektora jednostkowego o składowych n1,n2,n3 danych przez poniższe formuły (w kodzie Mathematica)
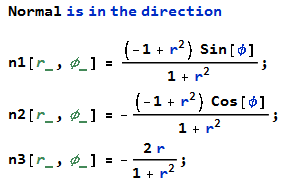
Okrąg przechodzący przez punkt r, φ można otrzymać w następujący sposób:
1) Malujemy okrąg o promieniu r0 i środku w zerze płaszczyzny z=0. Przekształcamy każdy punkt tego okręgu działając macierzą obrotu T1 daną formułą (w kodzie Mathematica) :
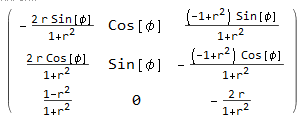
Wynik przesuwamy o (x0,y0,0).
A oto jak Mathematica maluje rodzinę tych okręgów dla r=0.2,0.4,0.6,0.8 i
φ zmieniającego się od 0 do 2π co π /10.
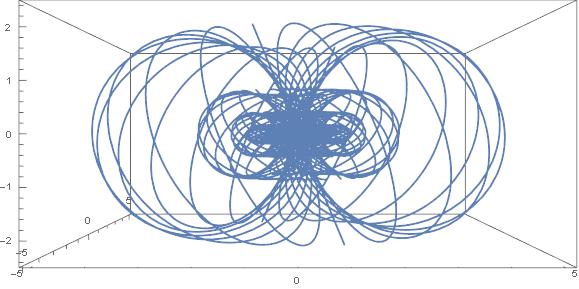
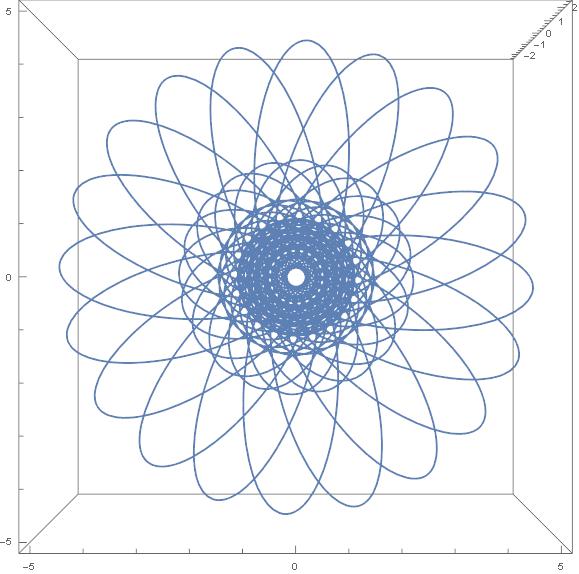
Jak na nowy rok – wyczyn to nie lada!
Pomyślności w Nowym Roku 2017 wszystkim moim Czytelnikom i Komentujacym!

