Już od dawna zapowiadałem pola. Teraz czas na nie. Zaczniemy powolutku, i powolutku będziemy się rozpędzać. Na końcu tej notki popłyniemy tak wartko, że nawet Tichy będzie miał problemy z nadążeniem. Zaczniemy od liczb zespolonych, jako, że prostsze są niż kwaterniony. W przedszkolu są tylko liczby zespolone. Kwaterniony przychodzą w pierwszej klasie podstawówki.
Więc mamy liczby zespolone
z = x + iy
Gdy t jest liczbą rzeczywistą, możemy utworzyć
u(t) = exp (it)
To zawsze można zapisać w postaci trygonometrycznej
u(t) = cos(t) + i sin(t)
Tak zdefiniowane u(t) leżą na okręgu jednostkowym |u(t)| = 1, co wynika z faktu, że cos2 t + sin2 t = 1.
Ja konsekwentnie jestem niekonsekwentny. Raz piszę cos(t), innym razem cos t. Nie mam w tym żadnej metody. Zatem cos2 t to to samo co cos(t)2 .
Jest jeszcze jedna miła własność: te nasze u(t) tworzą jednoparametrową grupę
u(t)u(t') = u(t+t'), u(0) = 1.
Widać to od razu z postaci u(t) = exp (it), by o tym się przekonać z postaci u(t) = cos(t) + i sin(t), trzeba trochę porachować.
Mnożąc liczby zespolone przez u(t) obracamy je:
z → z(t)= eit z
Zazwyczaj zamiast t piszemy greckie φ czy coś takiego. Wtedy mnożenie przez eiφ jest obrotem o kąt φ radianów w kierunku przeciwnym do kierunku ruchu wskazówek zegara. Mnożenie liczb zespolonych jest przemienne, zatem wszystko jedno czy z mnożymy przez eit ze strony lewej czy z prawej
eiφ z = z eiφ
Zaznaczam to celowo, bowiem dla kwaternionów , gdy do podobnych spraw dojdziemy, trzeba będzie uważać.
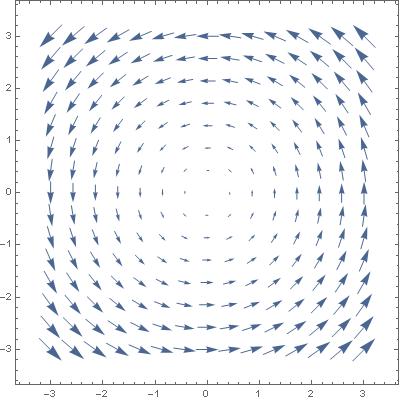
Każdy punkt z płaszczyzny zespolonej się teraz obraca. Ale jak szybko? By to zobaczyć rysujemy pole wektorowe prędkości. W tym celu liczymy
v(z) = dz(t)/dt wzięte w t=0.
Zapiszmy z = x+iy. Wtedy
z(t) = (cos t + i sin t)(x+iy)
Różniczkując po t
dz(t)/dt = (-sin(t) + i cos(t))(x+iy)
Kładąc t=0:
v(z) = i(x+iy) = -y+ix
Nasze pole wektorowe, zapisane na płaszczyźnie (x,y), ma więc składowe
v(x,y) = (-y,x)
Możemy je namalować.
Teraz, po tej rozgrzewce z liczbami zespolonymi przejdźmy do kwaternionów. Mamy teraz trzy niezależne jednostki urojone i,j,k. Przedtem pogrubiałem, teraz pogrubiania zaprzestanę. Kwadrat każdej z nich to -1, są też antyprzemienne:
ij = - ji = k,
ki = -ik = j,
jk = -kj = i .
Możemy teraz utworzyć trzy jednoparametrowe grupy (podgrupy grupy kwaternionów o normie 1):
u1(t) = exp (it) = cos t + i sin t
u2(t) = exp (jt) = cos t + j sin t
u3(t) = exp (kt) = cos t + k sin t
Możemy nimi kwaterniony przesuwać z lewej i z prawej
Lewe przesunięcie q → q(t) = u(t) q
Prawe przesunięcie q → q(t) = q u(t)
Będą nas interesowały pola wektorowe generowane przez lewe i prawe przesunięcia. Pole wektorowe generujemy różniczkując odpowiednie q(t) w t=0. Z różniczkowania u1(t),u2(t),u3(t) w t=0 otrzymamy odpowiednio i,j,k. Zatem lewe i prawe pola wektorowe to mnożenia przez i,j,k z lewej lub z prawej. No to wykonajmy to. Kwaternion q będziemy zapisywać nie jako
q = q0 +i q1 +j q2 + k q3
lecz jako
q= W + iX + j Y + k Z
Zaoszczędzi mi to pisania znaczków 1,2,3 przy składowych.
Lewe pole wektorowe z u1
i(W + iX + j Y + k Z) = -X + iW -jZ + kY
zatem
v1L(W,X,Y,Z) = (-X,W,-Z,Y)
Prawe pole wektorowe z u1 wyjdzie (korzystając z reguł mnożenia kwaternionów)
v1P(W,X,Y,Z) = (-X,W,Z,-Y)
Podobnie rachujemy v2 i v3. Każde z tych pól obraca niezależnie dwie pary współrzędnych. Możemy zrobić tabelkę
v1L = (-X,W,-Z,Y) , v1P = (-X,W,Z,-Y)
v2L = (-Y,Z,W,-X) , v2P = (-Y,-Z,W,X)
v3L = (-Z,-Y,X,W) , v3P = (-Z,Y,-X,W)
Zauważmy, że każde z tych pól ma zerowy iloczyn skalarny z wektorem wodzącym (W,X,Y,Z), jest więc równoległe do sfery kwaternionów jednostkowych – tych, co nas szczególnie interesują. Na przykład
(W,X,Y,Z).(-X,W,-Z,Y) = -WX+XW-YZ+ZY = 0
Ja wiem, że te pola to wyglądają na egzotyczne zwierzaki. Jednak, zapewniam, nie gryzą i nie dziobią. Czasem trochę kłują, gdy się pod włos usiłuje głaskać. Da się je udomowić, i wtedy nawet są miłe. Po pewnym czasie trudno bez nich żyć. W końcu one są w czterowymiarowej przestrzeni. A obłaskawienie czterowymiarowej intuicji jest, według Rudolfa Steinera, kluczem do rozwinięcia wyższych zdolności duchowych człowieka, zatem kluczem do Królestwa Niebieskiego. Z „Rudolf Steiner (1861-1925) - życie twórcy antropozofii”
Szczególnym przeżyciem stało się dla Steinera odkrycie geometrii, w której doświadczenie czysto duchowe potwierdzało jego dziecięce przeżycia paranormalne. (Po latach napisze: „Wiem, że w geometrii po raz pierwszy poznałem szczęście”.)
Wspominałem o tym kiedyś w notce Czwarty wymiar - Cienie i rzeczywistość.

S. Dali, W poszukiwaniu czwartego wymiaru.
W kolejnych notkach będziemy te nasze pola udomawiać, uczyć się ich zwyczajów, karmić i głaskać.

