Powrócę dziś do geometrii nieeuklidesowej, geometrii Bolyai-Łobaczewskiego, gdzie areną jest górna połowa płaszczyzny. Ktos mógłby pomyśleć, że jest to czysta matematyka, bez zastosowań, ot, taka zabawa. A jednak nie. Bowiem geometrię to, o dziwo, odnajdujemy w zagadnieniu Keplera ruchu planet czy w ruchu elektronu w polu protonu – problemie atomu wodoru. Ale o tym nie będę pisał. W każdym razie nie dziś. Dziś przygotuję grunt dla geometrii Riemanna na naszej półpłaszczyźnie – podam formuły na koneksję afiniczną bez torsji, odpowiedzialną za przenoszenie równoległe wektorów wzdłuż krzywych. (Jakich krzywych - zapyta tichy. Kawałkami różniczkowalnych).
W nocie „Torsja bez ariostii (powtórka - specjalnie dla tichego)„ opisałem prawo przeniesienia równoległego na półpłaszczyźnie wyposażonej w szczególny układ pól wektorowych, tzw. Reper, tyle że nieruchomy, więc jest to tylko geometria a nie dynamika. I pozostaniemy na razie przy geometrii. To prawo przeniesienia równoległego miało prostą własność – przeniesienie równoległe nie zależało od drogi po której przenosimy dany wektor. Krzywizna była równa zeru. To przeniesienie miało jednak dziwną własność: nie można było narysować kwadratu – boki się nie domykały. To zjawisko nazywa się torsją przeniesienia równoległego. Co to za przestrzeń z defektami? Nieestetyczna. Estetyka jest ważna, nie mówiąc już o zgodności z obserwacją. Dziś wrócimy więc do naszego problemu i wprowadzimy inne przeniesienie równoległe. To będzie miało niezerową krzywiznę, ale nie będzie miało torsji. Jest to bardziej estetyczne – z kilku powodów. Powodem pierwszym jest to, że krzywiznę łatwo możemy sobie wyobrazić, torsja to twór trudniejszy do wyobrażenia, wygląda nieco sztucznie. Powód drugi to to, że torsja jest samodzielnym obiektem – tensorem. W zastosowaniu do fizyki każdy taki samodzielny obiekt ma tendencję do reprezentowania czegoś istniejącego w Przyrodzie. Einstein miał przez pewien czas nadzieję (lata 30-te XX-go wieku), że torsja pasuje do pola elektromagnetycznego. Okazało się jednak, że nie pasuje. Nie pasowała do niczego. W czasach dzisiejszych mamy Rosjanina Shipova i jego kolegę Akimova, pracującego kiedyś dla rosyjskich służb specjalnych. Ci chcieli sprzedać ideę geometrii z torsją na Zachodzie. I owszem, Shipova na Zachód zaproszono, wyciśnięto z niego co się dało, i .... odrzucono. Bo Shipov nie tylko pokazywał matematyczne równania (oparte zresztą na błędach), lecz także urządzenia zabawki - „detektory i generatory pól torsyjnych”. Wiele jest ciekawych urządzeń, których działania nie daje się prosto wyjaśnić. Zachowania się zabawek Shipova ten nie potrafił wytłumaczyć. Poszły więc na półkę, do składu z innymi kuriozami. Akademik Krugliakow nazywa to pseudo-nauką i fałszywą nauką.
Tyle tytułem wstępu. Wracam teraz do górnej półpłaszczyzny i naszego układu pół wektorowych – tym razem z dodanymi okręgami, które mają przedstawiać jak jednostka długości zmienia się w zależności od punktu:
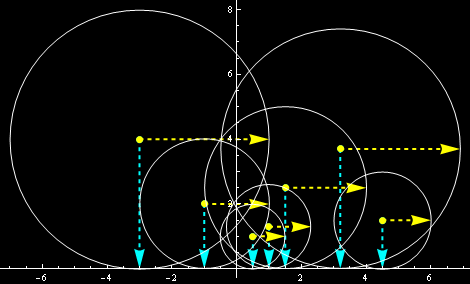
Promień okręgu jednostkowego o środku w punkcie (x,y) jest równy y. Przypomnę fragment z notki „Nieeuklidesowe koronki”
Czym bliżej osi x, czym mniejsze y, tym większe jest zagęszczenie. Czym dalej od osi y, tym większe jest rozciągnięcie. Napisać wzorami łatwo, zrobić na szydełkach znacznie trudniej – tylko niewielki kawałek da się wyszydełkować
A jak to jest wzorami? Nasze okręgi mają promienie równe y. Przypomnijmy, że macierz g reprezentująca elipsę o osiach a,b wzdłuż x-a i y-ka (nieprzekrzywioną) to
[1/a2 0]
[0 1/b2]
W naszym przypadku a=b=y, zatem nasza metryka g(x,t) to
[1/y2 0]
[0 1/y2]
Mamy więc metrykę Riemanna.
Mając metrykę moglibyśmy już znaleźć odpowiedź na pytanie: jak wygląda najkrótsza droga łącząca dwa punkty? Jest to kwestia rachunku wariacyjnego. Zadanie nietrudne. Pójdziemy jednak inną drogą. Miast pytac o to, jak wyglądają najkrótsze drogi, zastanowimy sie nad innym pytaniem: jak wyglądają najprostsze drogi? Okazuje się, że w geometrii Riemanna najprostsze drogi to to samo, co najkrótsze drogi, co jest estetycznie miłe. W teoriach z torsją tak nie jest. Nie oznacza to, że wszystko, co estetycznie miłe jest słuszne, zaś to, co zgrzyta jest niesłuszne. Jeśli jednak coś zgrzyta – musi ku temu być istotny powód. Chcemy wtedy zrozumieć dlaczego musi zgrzytać. Odkurzacz hałasuje. Jeden bardziej, drugi mniej. Pamiętam, miałem kiedyś odkurzacz polskiej produkcji, który nie tylko zgrzytał, ale wręcz wył. Przez pewien czas myślałem, że tak być musi, czym bardziej wyje, tym lepiej. To było kiedyś. Wczoraj odkurzałem małym, poręcznym odkurzaczem firmy Phillips. Ten przyjemnie szumiał, ciągną jak smok, w środku, za przezroczystą osłoną kręciło się coś w rodzaju wiatraczka, było widać ile jest w środku wirującego śmiecia – sama przyjemność!
Ale co to jest „najprostsza droga”? Iść „prosto” to „iść zachowując kierunek marszu”. Musimy więc umieć przenosić kierunki, przenosić wektory. Przenosić wzdłuż drogi po której się poruszamy. Nazywa się to „przeniesieniem równoległym. Potrzebne nam więc prawo przenoszenia równoległego. Potrzebna nam „koneksja afiniczna”. Dyskutowaliśmy już takie jedno prawo przy okazji torsji. Przypomnę z notki Torsja bez ariostii:
Koneksję afiniczną na rozmaitości zadaje się przez tzw „obiekt koneksji” Gamma. We współrzędnych x[mu] (mu=1,2,...n) ten obiekt zadany jest przez n^3 funkcji Gamma[mu,nu; sigma] (x), gdzie mu,nu,sigma = 1,...,n.
Nie będziemy się martwić tym, jak definiować koneksję afiniczną bez użycia współrzędnych. Można, ale nam to niepotrzebne.
Mając wektor (styczny) u = u[mu] w punkcie o współrzędnych x[mu] oraz krzywą x(t), zadaną we współrzędnych przez n funkcji x[mu](t), przechodzącą przez ten punkt z x[mu](0) = x[mu], przenosimy wektor u[mu] wzdłuż tej krzywej rozwiązując układ n równań różniczkowych zwyczajnych liniowych na n funkcji u[nu](t):
d u[sigma] (t)/dt + (suma po mu,nu ) Gamma[mu,nu;sigma](x(t)) u[nu](t) dx[mu](t)/dt = 0
z warunkiem początkowym u[nu](0)=u[nu]. W normalnie używanej notacji wygląda to tak
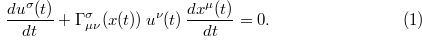
gdzie użyta jest tzw. konwencja Einsteina – sumujemy po powtarzających się wskaźnikach, gdy jeden jest na górze a drugi na dole.
Tym razem nie będziemy jednak żądać, by nasze pola wektorowe przenosiły się równolegle. Będziemy jedynie chcieli, by długość wektorów nie zmieniała się przy ich przenoszeniu. Jak to ująć matematycznie, w równaniach? Pominę szczegóły techniczne. Zauważę tylko, że w ogólności, w n wymiarach daje do n n(n+1)/2 równań. Koneksja ma n3 współczynników – to za dużo. Jeśli jednak zażądamy by koneksja była symetryczna (bez torsji), tzn. by Gamma[mu,nu; sigma] = Gamma[nu,mu; sigma] , wtedy mamy tyle samo równań co niewiadomych i szczęśliwie daje się ten układ równań jednoznacznie rozwiązać. W naszym konkretnym przypadku nasza beztorsyjna koneksja na półpłaszczyźnie Bolyai-Łobaczewskiego ma postać (wyprowadzenie pominę, ale na wyraźne żądanie mogę uzupełnić!):
1) Gamma[1,1;2] = 1/y
2) Gamma[1,2;1] = -1/y
3) Gamma[2,1;1] = -1/y
4) Gamma[2,2;2] = -1/y
Wszystkie inne Gammy sa zerami. W porównaniu z koneksją z torsją pojawiły się niezerowe współczynniki koneksji 1) i 2). Prawo przenoszenia równoległego się nieco skomplikowało. Nieco bardziej skomplikowane będą więc nasze „proste”. Okaże się, że będą okrągłe, no półokrągłe.








Komentarze