Wrócimy dziś, po dwóch tygodniach, do „Notki o torsji” - ale tym razem bez torsji. Przypomnę odpowiedni fragment z tej notki:
„Zapomnijmy na razie o parabolach i zajmijmy się światem lub areną w której parabole mieszkają. Ten świat to „górna półpłaszczyzna”. We współrzędnych są to punkty o współrzędnych (x,y), gdzie y jest większe od zera. Dnem tej półpłaszczyzny jest Prosta y=0. Półpłaszczyzna to obszar nad tą prostą.
Zbyszek P przyglądał sie tej półpłaszczyźnie i zapragnął wyposażyć ją w torsję. W końcu sam wielki Einstein pisał o torsji, o Fernparallelismus i o n-beinach, które Cartan nazywał repère mobile. W świecie parabol mamy n=2, będą to zatem dwunogi. Hmmm, zastanawiał się Zbyszek, jakie to dwunogi można wyhodować na półpłaszczyźnie, tak by rosły zgodnie z naturą? Jedyne co mu przyszło do głowy to dwunogi naturalne. Mając punkt (x,y) na górnej półpłaszczyźnie, tylko jeden naturalny wektor można z tego punktu poprowadzić: pionowo w dół, aż do Prostej, nazwijmy go e1. Wtedy można poprowadzić drugi naturalny wektor: poziomo w prawo, tej samej wielkości co e1, nazwijmy go e2. I stworzył Zbyszek dwa pola wektorowe: pole e1 wektorów pionowych i pole e2 wektorów poziomych. Wyglądało to jakoś tak, gdzie wektory pionowe są zielone a wektory poziome żólte:
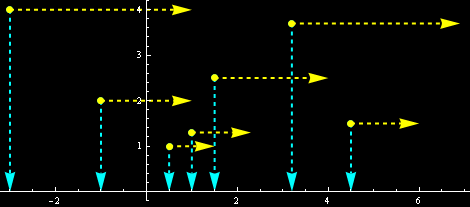
We współrzędnych można to zapisać jako
e1(x,y) = (0, -y)
e2(x,y) = (y, 0)
Tak postał Zbyszkowy Dwunóg.”
Dziś, kiedy mamy już jakieś mgliste wyobrażenie o tym, czym jest geometria Riemanna (choćby niech tylko w dwóch wymiarach) i czym jest metryka, możemy te Zbyszkowe idee oprawić w inne ramki. I od razu obraz nabierze innego wydźwięku.
Przypomnę z ostatnich notek, że zdanie geometrii Riemanna to nic innego niż narysowanie elipsy w każdym punkcie obszaru wyposażonego w jakieś współrzędne. Jak już wspominałem nie jest to całkiem ścisłe matematycznie, bo te elipsy winny być w „przestrzeniach stycznych”, nie będziemy się jednak tym przejmować, bowiem kawałek takiej przestrzeni stycznej da się zawsze utożsamić z kawałkiem płaszczyzny na której rysujemy siatkę współrzędnych. Dodatkowo, nie mam zamiaru zmieniać siatek współrzędnych, przechodzić od jednych do drugich – niech się tym martwią kartografowie i zawodowi geometrzy.
Elipsy w geometrii Riemanna obrazują nam rozciągnięcia i zwężenia jakim uległa przedstawiana we współrzędnych „powierzchnia” przy rozpłaszczaniu jej na płaszczyznę mapy. Elipsy są zatem obrazami pierwotnych okręgów o jednostkowym promieniu. W geometrii Euklidesowej, która jest szczególnym przypadkiem geometrii Riemanna, nic się nie rozpłaszcza. Płaszczyzna , z kartezjańskim układem współrzędnych, jest po prostu przykładana do siebie samej. Okręgi pozostają okręgami. Zatem obrazkowo geometria Euklidesa wygląda jakoś tak:
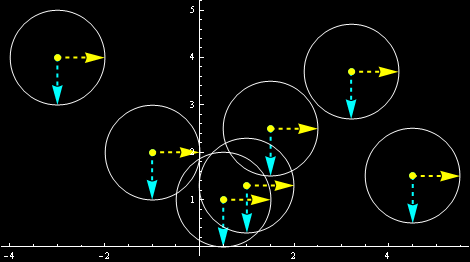
Elipsy są okręgami. Wektory „jednostkowe” (o „prawdziwej długości” jeden) są jednostkowe także na rysunku. Nic się nie rozciągnęło, nic się nie spłaszczyło. Macierz g przedstawiająca „metrykę” (patrz poprzednia notka) to macierz jednostkowa:
[1 0]
[0 1]
A jak to będzie z „geometrią Zbyszkową”? Traktując wektory Zbyszka jako osie elips otrzymamy taki obrazek:
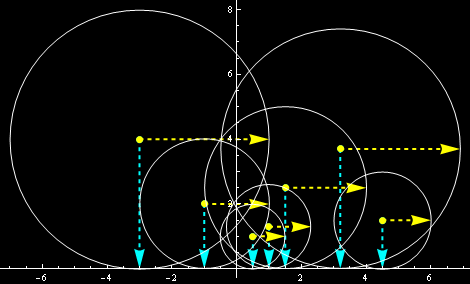
Okręgi są nadal okręgami – rozciągnięcie (czy spłaszczenie) jest takie samo w każdym kierunku – ale promień okręgu zależy od położenia jego środka. Dokładniej: jest równy wysokości środka okręgu nad osią x. Żeby coś takiego otrzymać przez spłaszczanie i rozciąganie jakby musiała wyglądać nasza pierwotna powierzchnia? Byłoby to coś takiego:
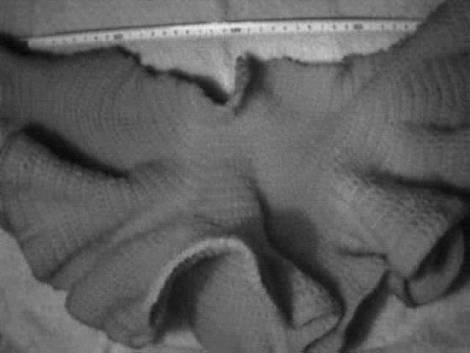
Czym bliżej osi x, czym mniejsze y, tym większe jest zagęszczenie. Czym dalej od osi y, tym większe jest rozciągnięcie. Napisać wzorami łatwo, zrobić na szydełkach znacznie trudniej – tylko niewielki kawałek da się wyszydełkować
A jak to jest wzorami? Nasze okręgi mają promienie równe y. Przypomnijmy, że macierz g reprezentująca elipsę o osiach a,b wzdłuż x-a i y-ka (nieprzekrzywioną) to
[1/a2 0]
[0 1/b2]
W naszym przypadku a=b=y, zatem nasza metryka g(x,t) to
[1/y2 0]
[0 1/y2]
Możemy teraz zacząć używać naszego matematycznego krzywomierza i mierzyć odległości. Zaczniemy od tych łatwych. Obliczmy odległość poziomego odcinka łączącego dwa punkty A i B, o współrzędnych (1,2) i (2,2) odpowiednio.
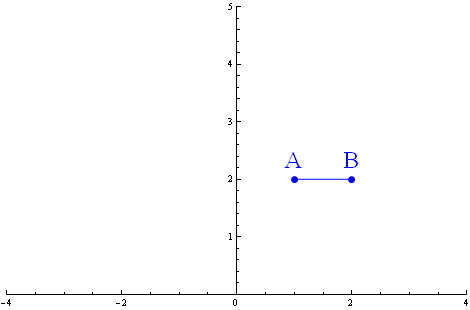
To zadanie jest łatwe. Cały nasz odcinek leży na wysokości y=2. Jednostka długości na tej wysokości wynosi także 2. Nasz odcinek to połowa tej jednostki długości. Zatem jego „prawdziwa długość” z szydełkowej robótki wynosi ½.
A teraz rozważmy odcinek pionowy. Tym razem nasze dwa punkty A i B to (1,2) i (1,1):
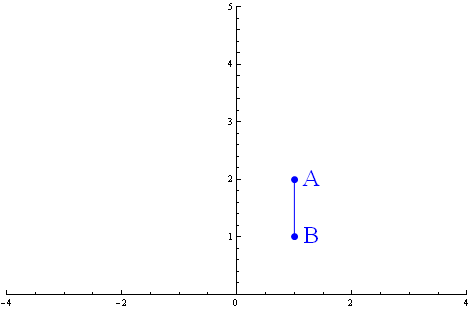
Tym razem skala zmienia gdy idziemy wzdłuż odcinka. Musimy użyć „metody całkowania” naszkicowanej w poprzedniej notce:
ds2 = g11(x,y) (Delta x)2 + g12(x,y) Delta x Delta y + g21(x,y) Delta y Delta x + g22(x,y) (Delta y)2 (formuła R)
Liczymy długość małego kawałka naszej linii. Wzdłuż całej linii x jest takie samo (równe 1). Zatem Delta x = 0. Podstawiając nasze dane redukujemy formułę do prostego:
ds2 = (1/y2) (Delta y)2
Będziemy szli nie od A do B, lecz od B do A – żeby y się zwiększało, wtedy Delta y będzie zawsze dodatnia. Ponieważ y jest u nas zawsze dodatnie, stąd
ds = (1/y) (Delta y)
Teraz trzeba te małe ds-y pododawać do siebie – wycałkować. Musimy wycałkować funkcję 1/y od 1 do 2. Ponieważ całkować mało kto umie, zajrzymy do Wikipedii pod całki z funkcji wymiernych (bo 1/y to funkcja wymierna). Znajdujemy tam, że całka z funkcji 1/x to log(|x|). U nas jest 1/y, zatem całka to log(|y|). Całkujemy od 1 do 2, stąd całka to log(2)-log(1). Kalkulatorem znajdziemy, że log(2)-log(1) to 0.693147. Zatem prawdziwa długość naszego pionowego odcinka to 0.693147.
A jaka jest prawdziwa długość pionowego gdy y zmienia się nie od 1 do 2 lecz od 5 do 6? Będzie to log(6)-log(5) = 0.182322.
A jaka jest prawdziwa długość pionowego odcinka gdy 6 zmienia się od 0.1 do 0.2? Będzie to log(0.2)-log(0.1) = 0.693147. Zatem prawdziwa długość odcinka gdy y zmienia się od 1 do 2 jest taka sama jak prawdziwa długość odcinka gdy y zmienia się od 0.1 do 0.2! I taka sama jest prawdziwa długość długość odcinka pionowego gdy y zmienia się 0.0001 do 0.0002! Niesamowite. Na naszym rysunku byłby to odcinek tyciutki-tyciutki. Czym bliżej osi y tym bardzie nasz rysunek musimy rozciągać by odtworzyć prawdziwą powierzchnię. Nic dziwnego, że szydełkowa robótka musi się coraz to bardziej fałdować.
I tak zaprzyjaźniliśmy się z pierwszym historycznie modelem geometrii nieeuklidesowej – geometrią Bolyai-Łobaczewskiego.
cdn








Komentarze