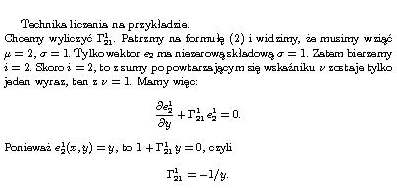Jako, że tichy nie zrozumiał mojej ostatniej notki, nie zrozumie jej nikt. To jest moja wpadka nad którą nie mogę przejść do porządku dziennego. Zatem raz jeszcze, powtórka, w stylu oszczędnym w słowa a precyzyjnym. Przygodny przechodzień będzie miał okazję poznać, mam nadzieję, że bez wstrętu, suchy język matematyki.
W ogólności o torsji mówi się gdy ma się do czynienia z n-wymiarową rozmaitością M wyposażoną w koneksję afiniczną, t.j. przepis na to jak przenosić równolegle wektory wzdłuż krzywych. W naszym przypadku rozmaitość to obszar otwarty w R^n, konkretnie górna półpłaszczyzna w R^2 we współrzędnych kartezjańskich, punkt x ma współrzędne x[mu], x[1] = x, x[2] = y.
Koneksję afiniczną na rozmaitości zadaje się przez tzw „obiekt koneksji” Gamma. We współrzędnych x[mu] (mu=1,2,...n) ten obiekt zadany jest przez n^3 funkcji Gamma[mu,nu; sigma] (x), gdzie mu,nu,sigma = 1,...,n.
Nie będziemy się martwić tym, jak definiować koneksję afiniczną bez użycia współrzędnych. Można, ale nam to niepotrzebne.
Mając wektor (styczny) u = u[mu] w punkcie o współrzędnych x[mu] oraz krzywą x(t), zadaną we współrzędnych przez n funkcji x[mu](t), przechodzącą przez ten punkt z x[mu](0) = x[mu], przenosimy wektor u[mu] wzdłuż tej krzywej rozwiązując układ n równań różniczkowych zwyczajnych liniowych na n funkcji u[nu](t):
d u[sigma] (t)/dt + (suma po mu,nu ) Gamma[mu,nu,sigma](x(t)) u[nu](t) dx[mu](t)/dt = 0
z warunkiem początkowym u[nu](0)=u[nu]. W normalnie używanej notacji wygląda to tak
gdzie użyta jest tzw. konwencja Einsteina – sumujemy po powtarzających się wskaźnikach, gdy jeden jest na górze a drugi na dole.
Przypuśćmy teraz, że na rozmaitości M dane jest n pól wektorowych e[i], i=1,...n, liniowo niezależnych w każdym punkcie, wtedy istnieje jedyna koneksja afiniczna dla której te pola wektorowe przenoszą się równolegle po dowolnych drogach. Obiekt koneksji można wyrachować z n^3 równań na przenoszenie równoległe. Te równania to
Wyrachowana z takich warunków koneksja afiniczna ma automatycznie krzywiznę zero (nie musimy wiedzieć co to krzywizna). Torsja koneksji to T[mu,nu,sigma] dana przez formułę:
T[mu,nu,sigma] = Gamma[mu,nu,sigma]-Gamma[nu,mu;sigma].
Przechodzimy do naszego konkretnego przypadku w dwu wymiarach. Nasze pola wektorowe e[1],e[2] to:
e[1](x,y) = (0,-y)
e[2](x,y) = (y,0)
Wtedy z równań (2) wyrachowujemy obiekt koneksji. Pomijam prosty rachunek. Otrzymujemy:
Gamma222 (x,y) = -1/y
Gamma211 (x,y) = -1/y
Wszystkie inne Gammy są zerami.
Możemy teraz przejść do „prostych” (autoparallels, geodesics). Sparametryzowana krzywa x(t) dana we współrzędnych przez funkcje x[mu](t) nazywa się „prostą”, gdy wektor styczny do tej krzywej u[mu](t) = d x[mu](t)/dt przenosi się wzdłuż tej krzywej równolegle. Innymi słowy równania (2) mają być spełnione gdy za u[mu](t) podstawimy tam d x[mu](t)/dt. Podstawiając otrzymujemy równania „prostych”:
W naszym przykładzie, podstawiając do równania „prostych” nasze Gammy, równania te sprowadzają się do dwóch następujących równań:
Drugie z tych równań ma ogólne rozwiązanie postaci:
y(t) = y0exp(ct)
gdzie c jest dowolną stała, zaś y0=y(0). Stąd obliczamy dy(t)/dt = cy0exp(ct) i podstawiamy do pierwszego równania. W rezultacie otrzymujemy:
x'' = cx'
gdzie ' oznacza pochodną po t.
Uwaga: Ten kawałek jest poprawiony w porównaniu z notą orygilną, bowiem tich znalazł niedoróbkę. Niedoróbka ta szczęśliwii nie wpływa jednak na rozumowanie, tylko je trochę komplikuje
Jeśli c= 0, to ogólne rozwiązanie tego równania to
x(t) =a t +x0
gdzie a jest stałą. Jeśli c jest różne od zera, wtedy ogólne rozwiązanie ma postać:
x(t) = a (exp(ct)-1)/c + x0.
Mamy więc ogólną postać „prostych”:
x(t) =a t +x0 lub x(t) = a(exp(ct)-1)/c + x0.
y(t) = y0exp(ct)
Podczas gdy x0,y0 to współrzędne punktu początkowego w t=0, stałe a,c są związane z prędkością początkową x'0,y'0. Widzimy, że
x'0 = a, y'0= cy0.
Stąd możemy dla każdego punktu i prędkości początkowej mamy „prostą” wychodzącą z tego punktu i z tą prędkością:
x(t) = x'0 t +x0 jeśli y'0= 0,
lub (gdy y'0 różne od zera)
x(t) = x'0y0 exp(ty'0/y0)-1)/ y'0 + x0
y(t) = y0 exp(y'0t/y0)
W naszym przykładzie rysujemy pionowo-poziomy kwadrat. Zatem zawsze albo x'0=0, albo y'0 =0. Gdy x'0=0, wtedy to drugie rozwiązanie dla x(t) to samo co pierwsze x(t) = x0, możemy więc o nim zapomnieć.
Koniec poprawionego kawałka.
Mając „proste” w jawnej postaci możemy skonstruować nasz „niezamykający się kwadrat”. Za prędkości początkowe będziemy brać nasze wyjściowe pola wektorowe wektorowe e[1] i e[2]. Pójdziemy po „prostych” najpierw wzdłuż e[2], potem wzdłuż e[1], oraz drugą drogą, najpierw wzdłuż e[1], potem wzdłuż e[2] i zobaczymy, że się nasz kwadrat nie zamknie. Każdy z naszych odcinków będzie miał „długość” epsilon, jeśli mierzyć ją parametrem t w naszych równaniach „prostych”.
Startujemy z punktu x0,y0 z prędkością początkową e[2](x0,y0) = (y0,0). Zatem x'0 = y0, y'0 = 0.Nasza „prosta” to
x(t) = y0t+x0
y(t) = y0
Kładąc t = epsilon otrzymujemy punkt (x1,y1) :
x1 = y0epsilon+x0
y1= y0
Teraz startujemy z punktu (x1,y1) i prowadzimy „prostą” w dół, w kierunku
e[1](x1,y1) = (0, - y1) =(0,- y0) . W równaniach
x(t) = x'0 t +x0
y(t) = y0 exp(y'0t/y0)
musimy za (x0,y0) podstawić (x1,y1), zaś za (x'0,y'0) podstawić (0,- y0). Otrzymujemy
x(t) = x1= y0epsilon+x0
y(t) = y1exp(-y0t/y1) = y0exp(-t)
Kładąc t = epsilon we get (x2,y2):
x2 = y0epsilon+x0
y2 = y0exp(-epsilon)
Wracamy do (x0,y0) i idziemy prosto w dół w kierunku e[1](x0,y0) = (0,-y0). W równaniach „prostych”
x(t) = x'0 t +x0
y(t) = y0 exp(y'0t/y0)
podstawiamy zatem x'0 = 0, y'0 = -y0. Dostajemy
x(t) = x0
y(t) = y0 exp(-t)
Podstawiamy t = epsilon i otrzymujemy punkt (x3,y3) :
x3 = x0
y3 = y0 exp(-epsilon)
Teraz startujemy z tego punktu w kierunku e[2] w tym punkcie. Wektor e[2] w tym punkcie to e[2](x3,y3) = (y3,0) =( y0 exp(-epsilon),0). W równaniach „prostych”
x(t) = x'0 t +x0
y(t) = y0 exp(y'0t/y0)
musimy podstawić (x3,y3) za (x0,y0) zaś ( y0 exp(-epsilon),0) za (x'0,y'0). Otrzymujemy:
x(t) = y0 exp(-epsilon)t +x0
y(t) = y0 exp(-epsilon)
Podstawiamy t = epsilon i otrzymujemy (x4,y4) :
x4 = y0 exp(-epsilon) epsilon +x0
y4 = y0 exp(-epsilon)
Porównujemy teraz z
x2 = y0epsilon+x0
y2 = y0exp(-epsilon)
Współrzędne y-kowe są takie same, ale x-owe są różne. Kwadrat się nie zamknął. Różnica wynosi:
x2 - x4 = y0epsilon(1-exp(-epsilon)).
Dla małych epsilon jest to
Defekt = y0epsilon2 + O(epsilon2)
Współczynnik przy epsilon2 to właśnie efekt nieznikającej torsji. Jest to bodaj najprostszy przykład i dobre ćwiczenie dla studentów lub do podręcznika.
Ostrzeżenie: powyższy rachunek jest dobry tylko dla przypadku gdy pola e[1], e[2] są polami równoległymi - jak to jest w naszym przypadku. W ogólniejszym przypadku (niezerowa krzywizna) trzeba by dotatkowo wektory przenosić równolegle wzdłuż boków kwadratu: wektor e[1] wzdłuż "prostej" w kierunku e[2] i wektor e[2] wzdłuż "prostej" w kierunku e[1].
Na zakończenie niezamykająca się pętla moich piesków:
Pieski są wyraźnie tą niezerową torsją sfrustrowane:

Na życzenie tichego dodaję przykład rachunku: