Pojęcie drogi i metody stosowanej przez księdza Palkigórnego wymagać będzie od nas dobrej woli i skupienia. Zajmie nam też trochę czasu. Przekonamy się jednak, że nie taki diabeł straszny jak go niektórzy księża (Palkigórnego tu wykluczam) malują.
Przez dany punkt P na krzywej przechodzi tylko jedna prosta styczna do tej krzywej (oczywiście narysowałem tylko mały fragment tej prostej):
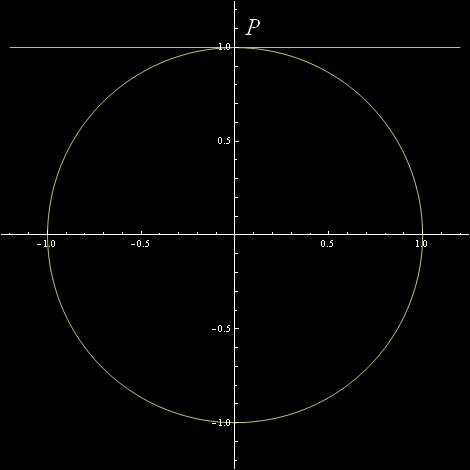
Na prostej stycznej można narysować jednak wiele różnych wektorów stycznych.
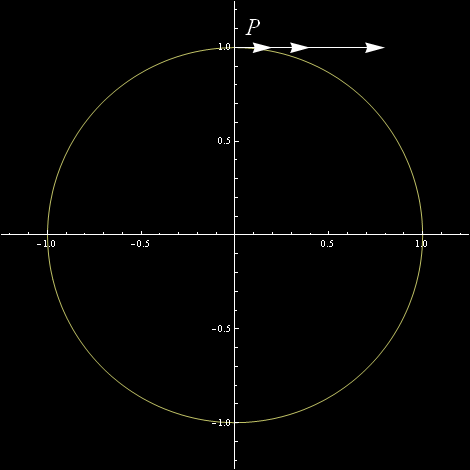
Wektor styczny do krzywej niesie w sobie informację o tym jak „szybko” obiegamy krzywą. Napisałem „szybko” w cudzysłowie, bo szybkość obiegu nie musi się wiązać z „czasem”. Możemy na przykład okrąg sparametryzować kątem mierzonym w radianach. By obiec okrąg potrzeba nam 2 Pi radianów. Możemy też jednak sparametryzować go katem mierzonym w stopniach. By obiec okrąg potrzeba nam 360 stopni. 360 to znacznie więcej niż 2 Pi – drobniejszy jest podział na stopnie niż na radiany. Łuk okręgu odpowiadający jednemu stopniowi jest znacznie mniejszy niż łuk odpowiadający jednemu radianowi. Zatem i wektor styczny do okręgu odpowiadający parametryzacji stopniami będzie znacznie krótszy od wektora stycznego odpowiadającego parametryzacji radianami. Konkretnie 360/(2 Pi), tj ok. 57 razy krótszy. Na obrazku, z zachowaniem prawdziwych proporcji, wyglądałoby to jakoś tak:
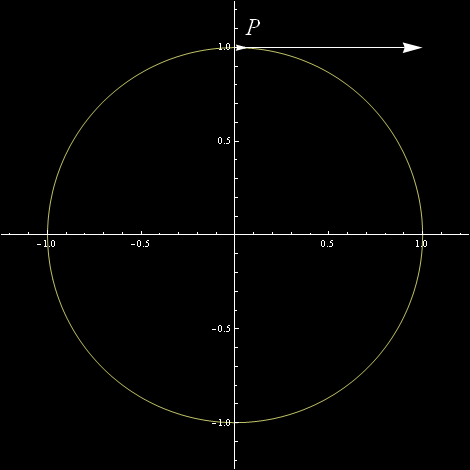
Choć się starałem, prawdziwych proporcji nie udało mi się zachować, bo tego krótszego wektorka w ogóle nie byłoby widać, nawet sama głowa jest za długa!
Wektory styczne możemy narysować nie w jednym a w wielu punktach krzywej. Oto „kilka” (ściślej: 24) wektorów stycznych obrazujących jednostajny obieg okręgu w parametryzacji w której pełen obieg to 2 Pi radianów.:
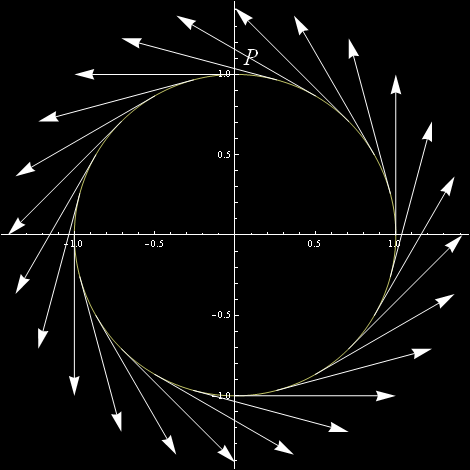
Nazywamy to „polem wektorów stycznych”. Dokładniej, o polu mówimy wtedy, gdy mamy wektor styczny w każdym punkcie krzywej. Tego jednak się nie da narysować, da się jedynie zasygnalizować, resztę musimy pozostawić wyobraźni.
Mówiąc językiem fizyków XX-go wieku operujących terminologią typową dla szczególnej i ogólnej teorii względności, wektor styczny to nic innego niż „lokalny układ odniesienia”. Wyznacza on on „jednostkę szybkości biegu czasu i jednostkę długości” w danym punkcie. Z niemiecka nazywa się to einbein (w czterowymiarowej czasoprzestrzeni vierbein) od bein – noga, ein - jeden. Jedna noga. W polskim znamy trójnóg, czemu nie jednonóg. Jedna noga – wektor styczny mówi nam o tym jak szybko mamy iść po krzywej. W formalizmie ogólnej teorii względności zadanie takich nóg w każdym punkcie krzywej określa pole grawitacyjne, zatem i „bieg czasu”. Narysowane wyżej „pole grawitacyjne” na okręgu wygląda na dość jednorodne – jego wektory mają na rysunku tą samą długość. Moglibyśmy narysować inne pole wektorowe odpowiadające niejednorodnemu (w geometrii rysunku) polu grawitacyjnemu, na przykład taki „oscylujący się” bieg czasu:
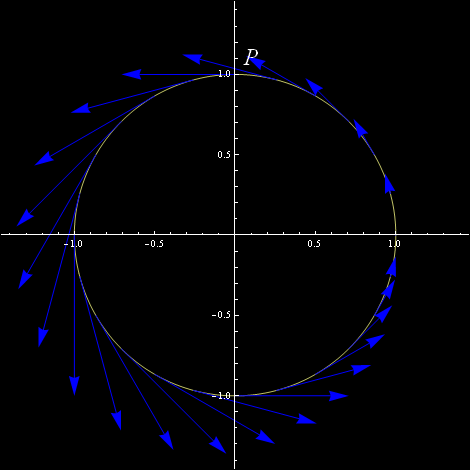
To płynie wolniej, to się rozpędza, to znów zwalnia. Dla liniaków mieszkających na okręgu, których serce bije w tym samym oscylującym rytmie, byłby to bieg czasu normalny, niczego, żadnej oscylacji czasu by nie zauważyły. Dopiero gdyby mogły porównać ze sobą dwa różne biegi czasu, to mogłoby by ich skłonić do zastanowienia się:
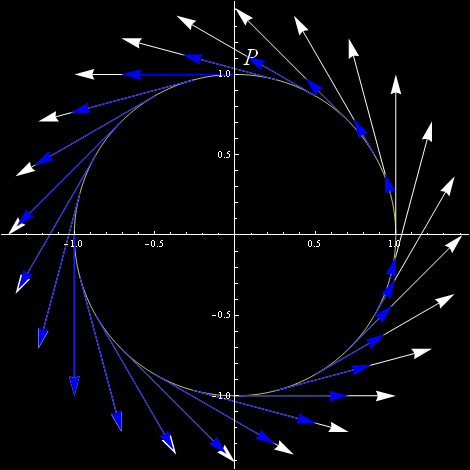
Trzeba powiedzieć, że w więcej niż jednym wymiarze jest inaczej. W jednym wymiarze wewnętrzna krzywizna krzywej jest zawsze równa zeru (nieważne, że jeszcze nie wiemy co to zwierz). Żyjątko na jednowymiarowej krzywej, kierując się tylko jednowymiarowymi zmysłami nie będzie w stanie stwierdzić, czy jakiś punkt na tej krzywej je przyciąga czy odpycha. Nam to nie będzie przeszkadzało, bowiem będziemy ze sobą porównywać różne pola wektorowe.
Wróćmy do księdz Palkigórnego. Ksiądz jak wiadomo musi umieć transformować. Z sutanny w marynarkę, z marynarki w sutannę. Z okręgu w prostą, z prostej w okrąg. Z okręgu w elipsę, z elipsy znów okrąg. Musi też, bezwzględnie, umieć operować parabolami. Palkigórny (nazywano go zdrobniale ksiądz Pagórek) świetnie sztukę transformacji opanował. Oto jak można sobie wyobrazić transformację okręgu w elipsę:
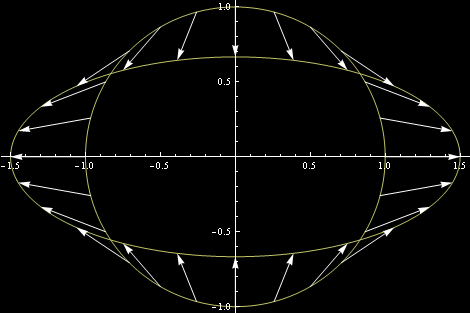
Można to zapisać wzorem. Na przykład na obrazku punkt okręgu o współrzędnych (x = cos(t), y = sin(t)) przechodzi w punkt elipsy (x= a cos(t),y = b cos(t)), gdzie za a wziąłem a = 1.5, za b zaś, b = 1/1.5. Okrąg po prostu przygniotłem – wyszła elipsa.
No dobrze, tak transformuje się okrąg. A jak przy tym transformuje się jego pole wektorowe? Jest jasne, że tam gdzie okrąg się rozciąga (na obrazku, powyżej i poniżej elipsy), tam odległości pomiędzy punktami rosną i pole grawitacyjne maleje. Tam zaś, gdzie punkty okręgu się ściskają, tam odległości pomiędzy punktami maleją, pole grawitacyjne (ściślej, natężenie pola) wzrasta. Jak to ująć wzorami? Bez pochodnych trudno. Podobnie jak bez łaciny. Nie będziemy tu uczyć ani łaciny ani pochodnych. Po prostu przetłumaczymy na „nasze”. Dla znających łacinę będą aptekarskie formuły, dla nie znających – wyjaśnienia formuł i obrazki. Reguła jest prosta: przetransformowane pole wektorowe to pierwotne pole wektorowe „pomnożone” przez pochodną transformacji. Weźmy np. parametryczne równanie okręgu (fizyk nazwie to ruchem jednostajnym po okręgu, lub ruchem harmonicznym z prędkością kątową równą 1):
x(t) = cos(t)
y(t) = sin(t)
Możemy na nie patrzeć jak na transformację z prostej (parametr t leży na prostej) w okrąg. (Uwaga: wystarczy nam tu dla t przedział [0, 2 Pi]) Na prostej mamy pole wektorowe styczne, które trudno narysować, bo wektor styczny do prostej leży na niej samej. Np. wektor styczny wychodzący z t=0 ma koniec w t=1, wektor styczny wychodzący z t=0.5 ma koniec w t=1.5 itd. Jeden na drugi powłazi przy próbie rysunku. Transformacja prostej w okrąg (sinusem i cosinusem, jak wyżej) transformuje to pole wektorowe w pole wektorowe styczne do okręgu. By je znaleźć, musimy obliczyć pochodne dx(t)/dt, dy(t)/dt. Otrzymamy
dx(t)/dt = -sin(t)
dy(t)/dt = cos(t)
Mnożąc przez 1 (to jednostkowe pole wektorowe na prostej) otrzymujemy składowe wektorów stycznych do okręgu. Teraz przypuśćmy, że rysujemy naszą elipsę a nie okrąg. Postępując podobnie jak wyżej otrzymamy dla elipsy obraz naszego jednostajnego pola wektorowego z prostej:
vx = -1.5 sin(t)
vy = cos(t)/1.5
Zatem pole wektorowe styczne do elipsy będzie miało początki w (1.5 cos(t), sin(t)/1.5)
a końce w (1.5 cos(t)+vx, sin(t)/1.5+vy) Na obrazku wygląda to tak:
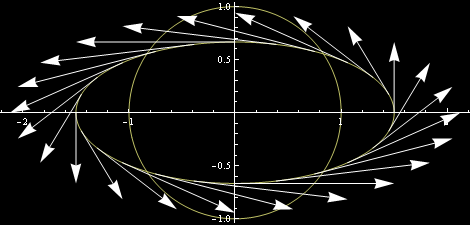
Tam, gdzie okrąg się wyciągnął, grawitacja na elipsie słabsza i krok (długość wektorów) się wydłuża – jak na Księżycu w porównaniu z Ziemią. Tam, gdzie okrąg musiał się ścieśnić, tam kroki stają się kroczkami, jak na Jowiszu w porównaniu z Ziemią.
Nie należy brać tych przenośni zbyt dosłownie, bo, jak zauważyłem, na krzywej jednowymiarowej takiej normalnej grawitacji, w sensie teorii grawitacji Einsteina, nie ma.
W kolejnym odcinku zrozumiemy jak ksiądz Palkigórny otrzymał z okręgu parabolę - Matkę wszystkich parabol. Ta parabola okaże się obrazem polem wektorowym, obrazem (przez odwrotną transformację Cayleya) jednostajnego, idealnego pola wektorowego na okręgu, jak na obrazku. Innymi słowy parabola Matka to nic innego niż obraz idealnie równomiernego „pola grawitacyjnego” na okręgu. Tyle, że najpierw nauczymy się jak uprościć sobie rysowanie pól wektorowych stycznych do krzywych.
cdn










Komentarze