Kurz Cantora

Fraktale bywają różnej maści. W ostatniej nocie pisałem o bodaj naprymitywniejszym z nich – fraktalu Cantora. Jest do tego stopnia prymitywny, że jego obrazek nie wzbudza żadnych emocji u nie-matematyków. A jednak jest pouczający.

Fraktale charakteryzują sie tym, że nie można im przypisać wymiaru, który jest liczbą całkowitą. W szczególności fraktal Cantora ma wymiar pomiędzy zerem - jak punkt, a jedynką – jak linia. A czemu jest równy jego wymiar? Dziś pokażę jak ten wymiar można wyliczyć na komputerze.

Matematyk wylicza wymiar fraktala Cantora bez komputera, natychmiast. Rozumuje tak: W każdej iteracji (patrz poprzednia nota) pojawiają się dwie kopie (dzieci) oryginału, każda z nich trzy razy mniejsza od oryginału. Stąd wymiar fraktala Cantora wynosi log(2)/log(3) = 0.63093... Ot i cała sprawa.

Zadanie: Używając tego samego przepisu - jaki jest wymiar fraktalny trójkąta Sierpińskiego?  

Ale aby zrozumieć czemu matematyk może być tak szybki, musielibyśmy zabrnąć nieco głębiej w matematykę. Moglibyśmy łatwo w niej utonąć. W dodatku taka prosta i szybka metoda stosuje się łatwo do jednych fraktali, podczas gdy do innych nie. Zresztą kto jest ciekaw, ten z łatwością znajdzie wyjasnienia w sieci. Dlatego pójdziemy inną drogą i zastosujemy przepis liczenia wymiaru lubiany przez uzytkowników komputerów. Recepta jest prosta i w miarę uniwersalna – prawie jak ciasto z książki kucharskiej. A że czasem wyjdzie zakalec, to już znana nam z własnego doświadczenia sprawa.

Najpierw nauczymy się generować „kurz Cantora” - przybliżający prawdziwy zbiór Cantora. Generuje się go podobnie jak trójkąt Sierpińskiego, o czym już pisałem poprzednio. Bierzemy odcinek [0,1] i dwie transformacje:

T1(x) = x/3

T2(x) = x/3 +2/3

Pierwsza transformacja przesuwa każdy x z naszego odcinka [0,1] w x z przedziału [0,1/3], druga zaś w x z przedziału [2/3,1]. Teraz tworzymy z tych dwóch transformacji iterowany układ funkcji (IFS) używając następującego algorytmu, gdzie random oznacza liczbę losową z [0,1]:

• wylosuj przypadkowe x z przedziału [0,1] jako punkt startowy

• powtarzaj 100 razy: jeśli random<1/2, x = T1(x) w przeciwnym razie x=T2(x)

To jest „rozbieg”. Taki rozbieg w IFS-ach zawsze się przydaje, aby nasz punkt trafił w pobliże „atraktora”. A dalej już powtarzamy wiele-wiele razy powyższy algorytm startując z x-a otrzymanego w wyniku rozbiegu. Wiele-wiele razy to np. N=1000 albo N=100000 albo N=100 mln. Zależnie od tego jakim sprzętem dysponujemy i jaki jest nasz cel. Tak powstaje „kurz punktów”.

Dobrze te wyniki gdzieś przechować, bo potem następuje ich obróbka. Oto pierwszy przykład takiej obróbki: podzieliłem odcinek [0,1] na 440 równych części i zliczyłem ile tego kurzu mieści się w każdej z tych części. Ponieważ wziąłem N=1 mln, na osi pionowej odłożyłem nie ilośc cząstek kurzu w każdej części, tylko logarytm przy podstawie 2 z tej liczby. Logarytmy w teorii fraktali i chaosu pojawią się zresztą raz po raz. Oto wykresik jaki otrzymałem:

 

 

Widać, że w samej rzeczy nic nie wpada do środkowego przedziału [1/3,2/3] ani też do środkowych podprzedziałów kolejnych potomków. Niewiele więcej z tego rysunku widać.

Dla porównania wygenerowałem 1 mln punktów czysto losowych. Obrazek wyglada tak:

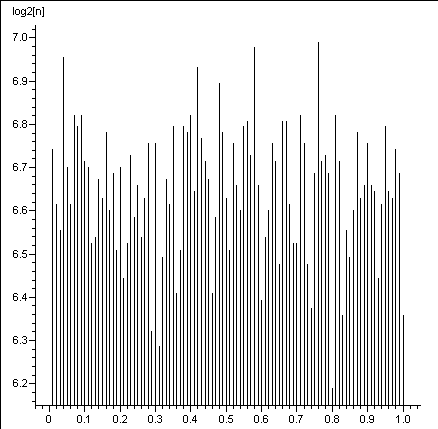
Rozkład w miarę jednorodny, choć jakby mój generator liczb losowych unikał z jakiegoś powodu okolic 0.3 i 0.8. Czy można takiemu ufać? Czy jest to przypadkowa statystyczna fluktuacja, czy też ewidentna niedoskonałość generatora? Nie będziemy się tym teraz przejmować, jako, że nie jest to istotne dla naszych celów. A celem naszym jest przybliżone wyliczenie z naszych wygenerowanych danych wymiaru „kurzu Cantora”.

W teorii fraktali dyskutuje się wiele róznych pojęć „wymiaru”. Najłatwiej wszak obliczyć tzw. „wymiar korelacyjny”. Recepta kulinarna jest prosta:

Przy ustalonej odległości r niech C(r) będzie liczbą par różnych cząstek kurzu odległych od siebie o mniej niż r. Powtarzając tą buchalterię dla coraz mniejszych r rysujemy wykres odkładając na osi poziomej log(r) a na osi pionowej log(C(r)). Jak wszystko pójdzie dobrze otrzymamy spory kawałek wykresu wyglądający jak linia prosta. Metodą najmniejszych kwadratów dopasowujemy do punktów z tego kawałka prostą i liczymy nachylenie delta y/delta x. Jest to „wymiar korelacyjny” naszego kurzu.

W praktyce zastosowanie tej metody wymaga sporo doświadczenia i wiedzy – jeśli chcemy uniknąć niespodzianek i błędów. Pomyślcie tylko: jeśli mamy milion punktów, to mamy milion milionów par. Dla każdej pary trzeba wyliczyć odległość i te odległości posortować do pudełek. Dochodzi liczenie logarytmów, za czym komputery nie przepadają, bo choć nam się wydaje, że logarytm wyliczany jest w mgnieniu oka, to jednak to mgnienie wymaga więcej pracy niż podniesienie liczby do kwadratu. Jest wiele róznych sposobów przyspieszenia tego wszystkiego. Na przykład znając wewnętrzną formę w jakiej liczby zmienno-przecinkowe są przechowywane w pamięci komputera nie musimy logarytmów wyliczać, bo ich część całkowita (eksponenta) jest już i tak przechowywana w pamięci jako część samej liczby. Nie będziemy w to się zagłębiać. Ja wziąłem r postaci 2^-k, gdzie k zmieniało się od 0 do 16. Zatem r=1/2, ¼, 1/8, 1/16, ...., 1/65536. Otrzymałem taki wykres dla bodaj 10000 punktów kurzu Cantora:

 

 

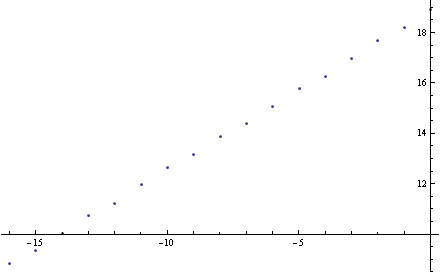
Wygląda to w istocie na linię prostą, nieprawdaż? Dopasowując otrzymałem nachylenie równe 0.630841. To „eksperymentalny wymiar korelacyjny” naszego fraktala Cantora. Przypomnijmy, że matematycznie wyliczony wynik dokładny wynosi log(2)/log(3) = 0.63093. Różnica na czwartym miejscu po przecinku przy tak „małej” próbce statystycznej – można powiedzieć „udało się”. Dla pewności zastosowałem tą samą metodę do całkowicie przypadkowego kurzu generowanego przez generator liczb losowych. Ten powinien być równomiernie rozłożony na odcinku, wymiar fraktalny powinie wyjść 1. Oto wykres jaki otrzymałem:

 

 

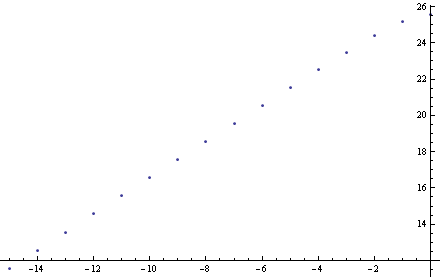
Dopasowując prostą otrzymałem nachylenie 0.97023. Raczej kiepsko, skoro powinno wyjść 1. Rasowy doświadczalnik czy statystyk przygląda się w podobnym przypadku swoim danym i wynajduje powody by część z nich odrzucić lub by "poprawić metodologię". Bo przecież doświadczenie musi pasować do teorii – inaczej pracy nie zaliczą lub nie przyjmą do druku. Nota bene zastanawiam się czasem ileż to prawdziwich odkryć nam umknęło na skutek takich właśnie nawyków.....

Na zakończenie tego odcinka większej całości notka o astronomii. Astronomowie kłócą się zawzięcie o to jaką strukturę ma nasz widzialny Wszechświat. Jest cała grupa astronomów spekulujacych na temat fraktalnej struktury Wszechświata. W tej grupie są podgrupy, a w tych podgrupach podgrupki – każda z nieco inną, choć podobną, koncepcją. Struktura iście fraktalna. Oto dla przykładu wykresiki wymiaru korelacyjnego „kurzu galaktyk” wzięte z pracy N.M. Celerier (Observatoire de Paris-Meudon) i R. Thiebergera (Ben Gurion University). Praca p.t. „Fractal Dimension of the Galaxy Distributions Varying in Steps?” (2004). Jak widać wymiar ten nie jest stały, jego szacowanie zmienia się w zależności od tego jaką skalę odległości weźmiemy. D₂ na obrazku to właśnie wymiar korelacyjny.

 

 

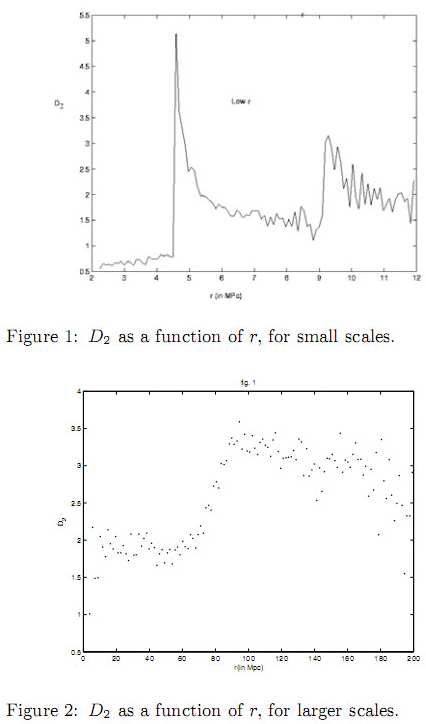
W następnej nocie zmienimy trochę prymitywny algorytm tworzenia fraktala Cantora i upodobnimy go do algorytmu z mechaniki kwantowej, gdzie prawdopodobieństwa przejść nie są stałe, lecz zależą od aktualnego stanu układu kwantowego.

cdn