Reanimacja Delty Diraca

Animacja czy reanimacja, to „ożywienie”. W Ewangeliach tak to wygląda:

„Jezus wzniósł oczy do góry i rzekł: Ojcze, dziękuję Ci, żeś Mnie wysłuchał. Ja wiedziałem, że Mnie zawsze wysłuchujesz. Ale ze względu na otaczający Mnie lud to powiedziałem, aby uwierzyli, żeś Ty Mnie posłał. To powiedziawszy zawołał donośnym głosem: Łazarzu, wyjdź na zewnątrz! I wyszedł zmarły mając nogi i ręce powiązane opaskami, a twarz jego była zawinięta chustą. Rzekł do nich Jezus: Rozwiążcie go i pozwólcie mu chodzić. „

W komentarzu do poprzedniej noty tichy się obruszył na to, że fraktale zaliczyłem do tworów statystycznych – nieżywych. Kiedy tak to własnie jest. Fraktal to zbiór. Zbiór jest martwy. Życie pojawia się dopiero wtedy, gdy coś się „rusza”. Przy czym, należy dodać, nie wszystko co się rusza jest żywe. A zresztą, czy ja wiem ....?

W poprzedniej nocie zacząłem pisać o najprostrzym iterowanym układzie funkcji (IFS), gdzy dana jest tylko jedna transformacja określona na przedziale [-1,+1] – dzielenie przez 2:

T(x) = x/2

Stosując ją wielokrotnie otrzymujemy coraz mniejsze przedziały, zdążamy do zbioru składającego się tylko z jednego punktu: x = 0. Tylko bowiem x=0 ma tę własność, że x/2 = x.

Lasota i Mackey, w swojej monografii, o której wspomniałem w poprzedniej nocie, sporo miejsca poświęcili operatorowi Perrona-Frobeniusa dla iterowanych układów funkcji. To bardzo ważny operator – będzie dla nas instrumentem wskrzeszenia Łazarza. Wskrzesimy dzis deltę Diraca. Powiemy: „delto wstań”, i delta wstanie. Ale najpierw musimy porozmawiać o miarach i wagach.

Weźmy nasz odcinek od minus 1 do plus 1. Jaką ma miarę? Jaką ma wagę? Niw iemy jak odpowiedzieć na to pytanie. Jedyne co nam przychodzi do głowy to to, ze ma długość dwa. Ale dlaczego właśnie dwa a nie trzy albo trzy i pół? Bo tak nas nauczono w szkole? Czy mamy przyjmować bez kwestionowania wszystko czego nas uczą w szkole? Przyroda nie wie co to jest odcinek. Możemy wziąć prosty kawałek drutu. Możemy go zmierzyć lub zważyć. Skoncentrujmy się na wadze. Ile waży nasz kawałek drutu? Powiedzmy, że waży 1 gram. Czy gdy przetniemy go na pół, to połowa będzie ważyć pół grama? Czasem tak, czasem nie. To zależy od tego, czy drut jest jednorodny czy nie. Zależy od tego, czy gęstość metalu jest stała czy nie. Bo może jedna połowa drutu jest wykonana z aluminium a druga z ołowiu? Ważna jest właśnie gęstość i jej rozkład wzdłuż drutu. Kierując się właśnie tego rodzaju rozumowaniem fizycy i matematycy wprowadzili pojęcie „miary” i „gęstości”. Nie chcę jednak wchodzić w zawiłości matematyczne. Miast tego rozważę po prostu przykład z naszą transformacją T(x) = x/2 określoną w przedziale [-1,+1].

Zacznijmy od prostego pytania: czy transformacja ta jest odwracalna czy nie? Na pierwszy rzut oka jest odwracalna. Przecież odwrotnoscią dzielenia przez dwa jest mnożenie przez dwa, nieprawdaż?

Prawda, ale nie cała prawda. Zapomnieliśmy bowiem o „ określoną w przedziale [-1,+1]”. Kiedy zatem pytamy o to, czy transformacja jest odwracalna czy nie, winniśmy, dla scisłości, dodać: czy jest odwracalna tak, że wynik transformacji odwrotnej leży w przedziale [-1,+1]? W zastosowaniu do ¼ odpowiedź brzmi „tak”, bowiem 2 razy ¼ to ½. Ale w zasosowaniu do ¾ odpowiedź brzmi „nie”, bowiem 2 razy ¾ to 3/2, a to leży poza naszym przedziałem. Rzecz w tym, że nasza transformacja T, choć jest wzajemnie jednoznaczna, nie jest transformacją „na”. Jest transformacją „w”. Odwrotność T jest okreslona tylko na obrazie odcinka [-1,+1] przez T, a tym obrazem jest odcinek[- ½,+ ½ ]. Tyle tytułem wstępu. Przejdźmy teraz do operatora Perrona-Frobeniusa związanego z iterowanym układem funkcji. Nie wchodząc w szczegóły: operator ten działa na gęstościach. Rozkład gęstości kawałka drutu może wyglądać na przykład tak:

 

 

To rozkład jednorodny. Może jednak wygladać też tak:

 

 

Tu największa gęstość jest w środku drutu i zmniejsza się ona w miarę zbliżania się do jego końców. I w jednym i w drugim przypadku „waga” drutu, jego „miara”, to pole po wykresem krzywej gęstości.

Niechaj g(x) będzie gęstością na odcinku X=[-1,+1], na przykład jak na ostatnim obrazku. Operator Perrona-Frobeniusa związany z transformacją T – oznaczamy go symbolem T* (gwoliścisłości matematycznej: gwiazdka winna być u dołu) dany jest wtedy przez następujacą, wyglądającą przerażajaco skomplikowanie, formułę:

(T*g)(x) = I_X(T^-1(x)) g(T^-1(x)) |dT^-1(x)/dx|, x należy do X

Ten paragraf jest tylko dla „zmatematyzowanych”: I_X to funkcja charakterystyczna zbioru X ( w naszym przypadku odcinka [-1,+1]). Jej obecność zabezpiecza istnienie transformacji odwrotnej w następujacych członach formuły. |dT^-1(x)/dx| to Jakobian transformacji odwrotnej – w naszym przypadku to po prostu 2.

To co nas interesuje, to wzięcie dowolnej gęstości g(x) i wielokrotne stosowanie do niej operatora T*.

Oznaczmy

g_n(x) = T*(T*(T* .....g)...))(x)

Trzeba to teraz zaprogramować, kazać komputerowi zrobić rysunek, rysunek pokazać.

Iteracje można programować na dwa sposoby: wprost lub stosując „rekurencję”. Co to jest rekurencja? Można zajrzeć do poskiej Wikipedii, gdzie można przeczytać:

„W logice wnioskowanie rekurencyjne opiera się na założeniu istnienia pewnego stanu początkowego oraz zdania (lub zdań) stanowiącego podstawę wnioskowania (przy czym aby cały dowód był poprawny zarówno reguła jak i stan początkowy muszą być prawdziwe). Istotą rekurencji jest tożsamość dziedziny i przeciwdziedziny reguły wnioskowania, wskutek czego wynik wnioskowania może podlegać tej samej regule zastosowanej ponownie.

Na prostym przykładzie:

reguła: każdy ojciec jest starszy od swojego syna; każdy ojciec jest czyimś synem

stan początkowy: jestem 22-letnim mężczyzną

teza: ojciec ojca mojego ojca jest starszy ode mnie

dowód:

1. mój ojciec jest starszy ode mnie

2. mój ojciec jest czyimś synem

3. ojciec mojego ojca jest starszy od mojego ojca

4. ojciec mojego ojca jest czyimś synem

5. itd.

Na przykładzie zastosowań matematycznych poniższa definicja ciągu Fibonacciego jest rekurencyjna: ...”

A także:

„Rekurencja jest podstawową techniką wykorzystywaną w funkcyjnych językach programowania.

Należy jednak zachować ostrożność przy używaniu rekurencji w rzeczywistych programach. Jeśli program nie jest w rzeczywistości rekurencyjny, to rekurencja może dramatycznie zwiększyć złożoność obliczeniową. Ponadto rekurencja zawsze zwiększa pamięciowe zapotrzebowanie programu ...”

Angielska Wikipedia ma notę znacznie ciekawszą, odwołuje się między innymi do znanej książki propagatora metod rekurencyjnych Douglasa Hofstadtera „Gödel, Esher, Bach” z następujacym zabawnym przykładem: Chcesz wiedzieć, co to jest rekurencja?

„Jeśli już wiesz, po prostu przypomniej sobie definicję. Jeśli nie wiesz, znajdź kogoś znającego Hofstadtera lepiej od ciebie i zapytaj go, co to jest rekurencja.”

W naszym przypadku stosujemy rekurencję w następujacy sposób: nie wiemy co to jest g_n(x), ale wiemy, że g_n(x) = T*g_n-1(x). Nie wiemy co to jest g_n-1(x), ale wiemy, że g_n-1(x) = T*g_n-2(x). I tak moglibyśmy iść w nieskończoność gdyby nie to, że decydujemy iż np. g₀(x) to funkcja tożsamościowo równa jedności – gęstość jednorodna, jak na pierwszym z obrazków gęstości. Pozostaje nam zaprogramowanie tego. Nie każdy język programowania pozwala na to by funkcja, w swej definicji, odwoływała się do swej własnej definicji. Prymitywny Basic na to nie zezwalał. Dzisiejszy np. FreeBasic na to pozwala. Mógłbym go więc użyć. Jednak tego nie zrobię, potrzebne mi bowiem wkrótce będą przyrodzone możliwości graficzne programu. Dla wykresów dwu-wymiarowych dałbym sobie z łatwością rade nawet z Bejzikiem. Ale już dla obrazków trójwymiarowych musiałbym ładować dodatkowe pakiety graficzne lub eksportować dane liczbowe do innych graficznych programów. Szkoda zachodu. Uzyję więc programu Mathematica, który ma to wszystko już wbudowane.

Definicja funkcji g wygląda tak:

 g[x_Real,n_Integer]:=Module[{i=n,T1,y},

  T1[y_]=2 y;

  If[i==0,1,

   If[T1[x]>-1 && T1[x]<1,

    2*g[T1[x],i-1],0],0

   ]]

Należy to czytać tak:

Przez T1 oznaczyłem transformację odwrotna do T. Zdefiniowana jest przez

T1[y_]=2 y. Wskaźnik i numeruje kolejne, idące w dół, stopnie rekurencji. Następnie program robi tak: jeśli jesteś na końcu rekurencji, wtedy g(x) jest jedynką. Jesli jeszcze na końcu nie jesteś, to sprawdż czy T^-1(x) leży w naszym odcinku. Jeśli leży to oblicz 2g(x,i-1), jeśli nie leży, wartością jest zero.

Oto kolejne wykresy funkcji g₀,g₁,g₂,g₃:

 

 

 

 

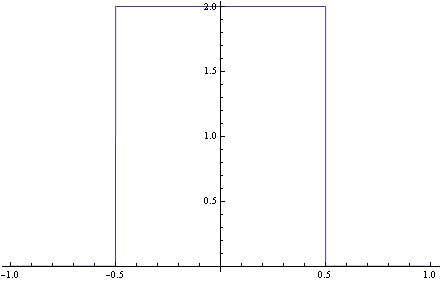
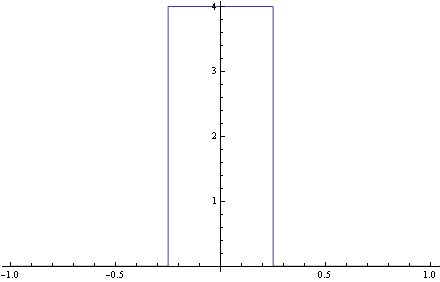
A oto animacja gn(x) dla n zmieniajacego się od zera do sześciu:

 

 

Mathematica robi ją w dwóch krokach:

 pt=Table[Plot[g[x,k],{x,-1,1}, 
PlotPoints->1000, PlotRange->{0,2^6}], 
{k,0,6,1}]

 Export["C:\deltad.gif",pt,ImageSize->440, 
AnimationRepetitions->Infinity]

I tak ożywiliśmy Łazarza. Operator Perrona-Frobenius nie tylko rysuje fraktal (w naszym przypadku tylko jeden punkt – punkt zero), ale przybliża nam „niezmienniczy rozkład gęstości” na tym fraktalu. W naszym przypadku są to kolejne przybliżenia delty Diraca.

Ciekawiej będzie to wygladało dla trójkąta Sierpińskiego a jeszcze ciekawiej dla „fraktali kwantowych”. Ale o tym w kolejnych notach.

Czy są pytanie? Rozglądam się po sali. Sala opustoszała. Pytań nie ma ....

Uwaga techniczna: Operator Perrona-Frobeniusa nazywany jest czasem operatorem Markowa, czasem zaś określa się go mianem „transfer operator”. Zwykle stosuje się go do miar, nie do gęstości tych miar, jak u mnie. Miarę jednak trudno narysować (to funkcja zbioru), gęstośc miary to po prostu funkcja, więc jej wykres narysować można.