Do czego przydają sie liczby zespolone? Dziś możemy dać prostą odpowiedź: przydają się do produkcji fraktali. „A ile trzeba zainwestować w taka produkcję?” - zapyta Czytelnik. Niewiele, o czym w dzisiejszym nocie zechcę przekonać. Zacznę od liczb zespolonych i od znanego powszechnie z obrazków zbioru Mandelbrota – to w następnej nocie. A w jednym z następnych wpisów mam zamiar dojść do fraktali kwantowych – jednego z rodzimy, bo polskich, odkryć.
Najpierw liczby zespolone. By je opanować konieczna jest jedynie znajomość mnożenia i dodawania, no także pewna sprawność w tym zakresie. Ułamki się też przydadzą.
Liczba zespolona z to nic innego niz wyrażenie postaci
z = x+yj
Tutaj x,y to są „zwykłe liczby”, liczby rzeczywiste. Zaś j to symbol o którym jedyne co trzeba wiedzieć to to, że j do kwadratu, tzn. j razy j, to minus jeden:
j2 = jj = -1
Poza tym obowiązują zwykłe reguły mnożenia i dodawania.
Mając dwie liczby zespolone, n.p.
0.5+0.75j
0.3-2j
Mozemy je dodać:
(0.5+0.75j)+(0.3-2j) = 0.5+0.75j+0.3-2j
następnie zebrać współczynniki bez j oraz te z j:
(0.5+0.3)+(0.75-2)j
i otrzymamy nową liczbę zespoloną – sumę naszych dwóch liczb:
0.8-1.25j
Niczym się to nie różni od dodawania wektorów (np. sił) według reguły równoległoboku.
Liczby zespolone zatem to nic innego niż wektory na płaszczyźnie. Liczbę x+yj przedstawiamy jako wektor o współrzędnych (x,y):
Tak jak i wektor, tak i liczbę zespoloną z można opisać podając jej „długość” i kąt jaki tworzy przedstawiajacy ją wektor z osią x. Długość tego wektora przedstawiającego liczbę z, zwaną także modułem z, oznacza się zazwyczaj symbolem |z|, lub Abs(z). Kąt zaś nazywa się fazą (także argumentem, arg(z)) liczby z. Rysunek w poprzedniej nocie, ale pokażę go tu jeszcze raz:
Liczby zespolone można też mnozyć jedną przez drugą by otrzymać nową liczbę zespoloną – ich iloczyn. Jedyne co trzeba wiedzieć by można było mnozyć jedną liczbę zespoloną przez inną to to, że j razy j to -1.
Zatem:
(0.5+0.75j)(0.3-2j) =
(0.5)(0.3)+(0.5)(-2)j+(0.75j)(0.3)+(0.75j)(-2j) =
0.15-j+0.225j+1.5 = 1.65-0.775j
Można zapytać czemu taka reguła mnożenia? Reguła ta ma prostą interpretacją geometryczną. Przy mnożeniu liczb zespolonych długości przedstawiających ją wektorów się mnożą, zaś fazy się dodają. Tak to wyglada na obrazku na przykładzie mnożenia j = 0 + 1j przez siebie:
Wektor przedtstawiający j ma długość 1, zatem jj też będzie miał długość 1 (1 razy 1 jest 1). Wektor przedstawiajacy j tworzy kąt 90 stopni z osią x, zatem wektor przedstawiający j do kwadratu będzie miał fazę 90+90=180 stopni. A to jest właśnie minus jedynka na osi x. Stąd i reguła wyjściowa: j do kwadratu to minus jeden!
Przy dodawaniu faz, które są miarami kątów, trzeba trochę uważać. Kąty opisujemy albo w stopniach, albo w radianach. 360 stopni to 2Pi radianów. Jesli uzywamy stopni, jesli jedna faza to 120 stopni a druga to 300 stopni, dodając wyjdzie nam 420 stopni. To więcej niż 360! Trzeba pamiętać, że po 360 stopniach wracamy do punktu wyjścia i liczenie zaczyna się od zera. Zatem 420 stopni to to samo co 420-360 = 60.
Podobnie minus 10 stopni, to to samo 360-10 = 350 stopni. Podobnie z radianami, tyle, że 360 trzeba zastąpić przez 2Pi.
Mając liczbę zespoloną z=x+yj, liczbę x (współrzędną x-ową wektora) nazywamy częścią rzeczywistą liczby z i oznaczamy symbolem Re(z) („Re” od „real”, rzeczywisty), zaś liczbę y (współrzędną y-kową wektora) nazywamy częścią urojoną liczby z i oznaczamy symbolem Im(z) („Im” od „imaginary”, urojony). Nic urojonego zresztą w tym igreku nie ma. Jest tak rzeczywisty jak i x. Ot, tradycja.
Przy dodawaniu liczb zespolonych z osobna dodają się częsci rzeczywiste i zespolone:
Re(z1+ z2) = Re(z1) + Re(z2)
Im(z1+ z2) = Im(z1) + Im(z2)
Nie ma pomiędzy nimi „oddziaływania”. Przy mnożeniu jest inaczej. Następuje oddziaływanie i stąd się bierze piękno i głebia liczb zespolonych. Porachujmy. Pomnóżmy przez siebie liczby zespolone z1 i z2.
z1=x1+y1j, z2 = x2+y2j
z1z2=(x1+y1j)(x2+y2j)=x1x2+x1y2j+x2y1j-y1y2= (x1x2-y1y2)+(x1y2+x2y1)j
Możemy to zapisać jako:
Re(z1z2) = Re(z1)Re(z2) – Im(z1)Im(z2)
Im(z1z2) = Re(z1)Im(z2) + Im(z1)Re(z2)
W szczególności liczbę zespoloną z=x+yj można podnieśc do kwadratu, czyli pomnożyć przez siebie. Co wyjdzie?
A) Re(z2) = Re(zz) = Re(z)Re(z) – Im(z)Im(z) = Re(z)2 – Im(z)2
B) Im(z2) = Im(zz) = Re(z)Im(z) + Im(z)Re(z) = 2Re(z)Im(z)
Te dwie formuły A), B) zaraz nam sie przydadzą. Przechodzimy bowiem do budowania fraktala - zbioru Mandelbrota. Zbudujemy go następnym razem. Najpierw zabawmy się trochę. Punktem wyjścia jest prosta formuła. Ustalmy liczbę zespoloną c, powiedzmy
c = -0.75 + 0.1j
Będziemy rozważać tranformacje liczby zespolonej z opisane formułą:
Nowe z to stare z do kwadratu plus c:
T(z) = z2+c
Zacznijmy od z = 0.
T(0) = 02+c = c = -0.75 + 0.1j
Zastosujmy tą transformację jeszcze raz:
T(T(0)) = c2+c
T(T(T(0))) = (c2+c)2+c
(T(T(T(0)))) = ((c2+c)2+c)2+c
Obliczanie tego ręcznie jest bez sensu. Od tego jest komputer, nieprawdaż. Oznaczmy przez Tn(0) wynik po n-krotnym wykonaniu trensformacji T. Pokażę na obrazku punkty powstały po 33 transformacjach. (Uwaga: kiedy wielokrotnie, tak jak powyżej, tą samą transformację, mówimy o iteracjach). Dlaczego po trzydziestu trzech? Zaraz się okaże. Iterujemy więc transformację T, wychodząc z punktu z = 0. Oto wyniki kolejnych trzydziestu trzech iteracji:
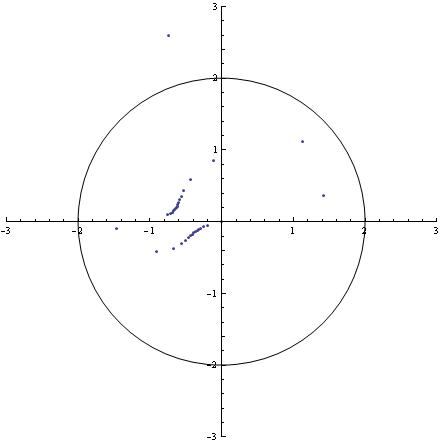
Na obrazku narysowałem też okrąg o promieniu równym 2. Do trzydzietej drugiej iteracji z grzecznie siedziało w kółku o promieniu 2. Przy 33-ciej z niego uciekło. Trochę algbery i można udowodnić, że jesli nasze z raz ucieknie z tego kółka o promieniu 2, to już do niego nie wróci, i to niezależnie od wartości stałej c. Nie będziemy się w to wgłębiać.
Liczba 33 jest ciekawa, nieprawdaż? Spróbujmy zatem z innym c, tym razem weźmy
c = -0.75 + 0.01j.
Ile iteracji n trzeba, by Tn(z) uciekło z kólka? Eksperyment komputerowy, dość prosty zresztą, pokazuje, że trzeba ich .... 315. Oto wynik. Trzysta pietnaste z już poza kólkiem.
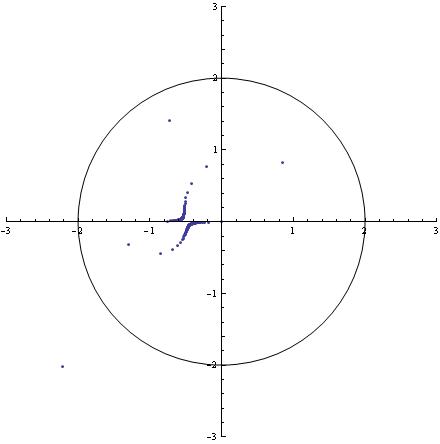
Hmmm, prawidłowość jakaś? Odzywa się w nas żyłka eksperymentatora. Czemu nie wziąć c = -0.75 + 0.001j? Więc wziąłem. Oto wynik:
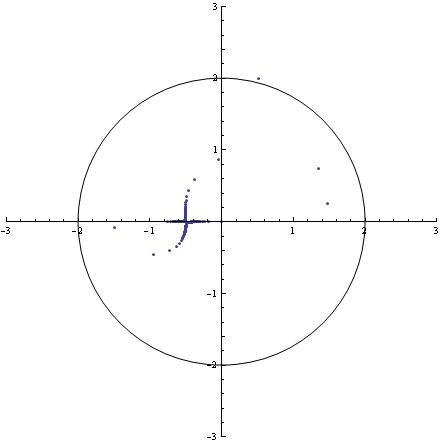
Tym razem to za 3143 -cią iteracją nasz punkt uciekł z kólka. W istocie, jakby jakaś prawidłowośc:
0.1 razy 33 = 3.3
0.01 razy 315 = 3.15
0.001 razy 3143 = 3.143
Znając jakiś język programowania (o tym w następnej nocie, będzie tym moim wybranym językiem Basic, konkretnie „FreeBasic” - do sciągniecia tutaj, wyjaśnię też jak się z tym zwierzakiem obchodzić) można poeksperymentować trochę dalej. Nie zdradzę chyba wielkiej tajemnicy, jeśli powiem, ża dla c = -0.75+0.0000001j ucieczka następuje przy 31415927-ej iteracji, oraz, że
0.0000001 razy 31415927 = 3.1415927
Jakby coś chciało wyjść, jakaś tajemnicza liczba? Czyżby Pi? Czy odkryśliśmy coś nowego tak się bawiąc? No, nie tym razem. Odkrycia tego dokonał niejaki Dave Boll w roku 1992. Trzeba było trochę czasu by ktoś się tym zainteresował, potem jeszcze trochę czasu zanim zaczęto to jakoś rozumieć. (patrz pdf link na początku). Widzimy stąd, że w matematyce na każdym kroku możemy odkryć nowe, zaskakujące i niepodejrzewane prawidłowości. Można je odkryć bezstressowo, po prostu dobrze się bawiąc tak jak zapewne bawił się Fermat obwieszczając potomnym o swoim słynnym spostrzeżeniu dotyczącym liczb pierwszych. Jeśli się nie staniecie jako te dzieci, nie wnijdziecie do Królestwa Niebieskiego!
Uwaga: w tekście było kilka błędów. W szczególności, co najważniejsze, zapomniałem zanku minus przy podanych wartościach stałej c. Już to poprawiłem.
Cdn.

