Perspektywy

Meandruję. Miałem przenieść transformacje geometryczne przesunięcia, odbicia, skalowania i inwersji z prostej na okrąg. Miałem zamiar użyć do tego algebry. Po namyśle jednak doszedłem do wniosku, że nie jest to najlepsza droga. Nie daje bowiem intuicji. A intuicje są niezmiernie ważne. Czasem nawet ważniejsze od praktycznych recept. Bez intuicji ani rusz, nie ma mowy o twórczości. Do wyrobienia intuicji najlepiej nadają się obrazki. Może to właśnie dzięki myśleniu obrazami mamy przewagę nad komputerami?

Warto też zawsze sięgnąć do źródeł. Nie zawsze jest to możliwe. Kiedy jest to możliwe, wtedy należy. W tym przypadku jest to możliwe. A geometria ma swe źródła w naszym postrzeganiu wzrokowym. Nie tylko zresztą geometria. Także sztuka: malarstwo, rzeźbiarstwo, architektura. Kluczem jest tu światło oraz nasze widzenie. Kluczowym słowem jest „perspektywa”. Demonstruje ją najprościej poniższy typowy obrazek:

 

 

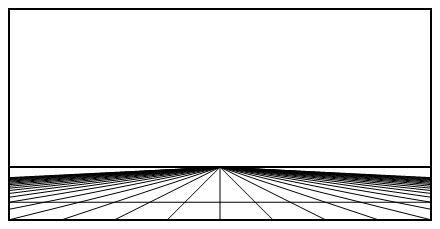
Rys1. 

Potrzebna nam będzie, w tym cyklu, jedynie okrojona wersja perspektywy – w dwóch wymiarach. To i dobrze, bo grafika będzie prostsza. Najpierw wyciągnijmy najważniejsze dla naszych celów z powyższego obrazka.

Mamy dwie równoległe linie, jedna będąca wierną kopią drugiej, i źródło światła. Wyposażmy te linie w podziałkę.

 

 

 

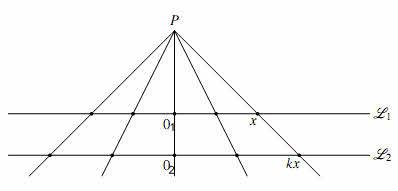
Promień wychodzący z punktu P przechodzi przez punkt x na linii L₁ i zostawia ślad w punkcie kx na linii L₂. Mamy transformację skalowania. Współczynnik skalowania łatwo wyliczyć z podobieństwa trójkątów PO₁x i PO₂kx: jest równy stosunkowi odległości PO₂/PO₁. Tak otrzymaliśmy transformację skalowania S_k(x) = x.

A teraz bądźmy elastyczni. Pozwólmy obu liniom być w dowolnym położeniu względem siebie a także pozwólmy źródłu światła znaleźć się w dowolnym miejscu, nawet bardzo, bardzo daleko – w nieskończoności, coś takiego:

 

 

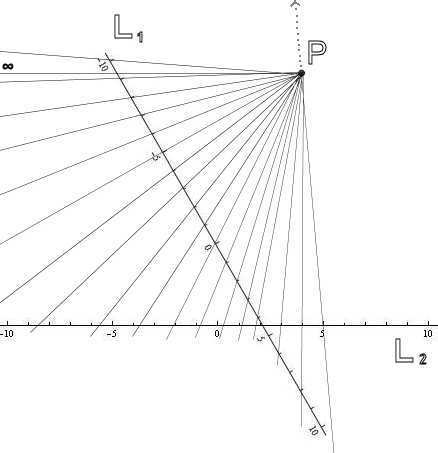
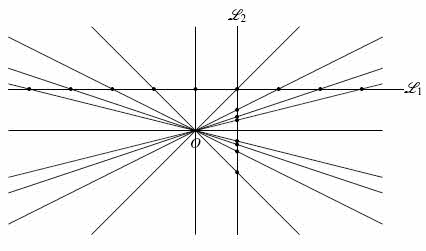
Jakiego rodzaju transformacje otrzymamy? Oznaczmy naszą transformację z obrazka literą W

Przyjrzyjmy się najpierw promieniowi przechodzącemu przez x = 0 na lini L₁. Ten trafia mniej więcej w -2 na linii L₂. Mamy więc W(0) = -2. Linia przechodząca przez x = 6 na L₁ trafia mniej więcej w 3 na L₂. Zatem W(6) = 3. Widzimy też, że W(8) = 4, W(11) = 5, co już wychodzi poza obrazek. Wszystko to w przybliżeniu, bowiem z obrazka nie potrafimy odczytać dokładniej.

Zauważmy, że dzieje się ciekawe rzeczy. Podczas gdy promień przechodzący przez x = 0 przechodzi najpierw przez linię L₁ i następnie trafia w linię L₂, to promień przechodzący przez x = 11 na L₁ trafia najpierw w L₂, dopiero potem w L₁. Trochę to dziwne. Najpierw obraz, dopiero potem punkt którego obraz rysujemy? Wyjście z tego paradoksu polega na użyciu wyobraźni. Możemy bowiem sobie wyobrazić, że promień wychodzi z punktu P w obu kierunkach. Kropkami zaznaczyłem ten przeciwny kierunek. Promień ucieka „do nieskończoności”, poza górna krawędź obrazka, i wraca z drugiej strony, pojawia się u dołu, trafia w L₁, w x = 11, a następnie w L_2.

Druga ciekawa rzecz dzieje się, podążając za kolejnymi promieniami od prawej do lewej, po przekroczeniu x = -9, gdzieś koło x=-9.25 na L₁. Promień staje się tam równoległy do L₂, nie zostawi więc na L₂ żadnego śladu! Wyjście z tej sytuacji polega znów na dodaniu nieskończoności. Zostawi ślad w punkcie nieskończoność! Nieskończoność zatem jest przydatna.

Czy potrafimy zapisać naszą transformację z obrazka jednym wzorem? Najlepiej prostym?

Nim postaramy się odpowiedzieć na to pytanie przedstawmy najpierw obrazkowo transformacje translacji Ta(x) = x+ a, oraz inwersji konforemnej C(x) = 1/x:

 

 

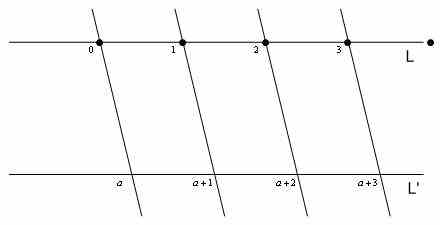
Rys 4.Translacja – rzut równoległy. Źródło światła w nieskończoności.

Nasza transformacja W będzie pewnie złożeniem tych prostych transformacji .... Co możemy dostać z takiego składania? Najpierw, powiedzmy, przeskalujmy x, S_k(x) = kx. Następnie przesuńmy wynik o a: T_a(S_k(x)) = kx+a. Następnie dokonajmy inwersji:

C(T_a(S_k(x)) ) = C(kx+a) = 1/( kx+a). (1)

Bawiąc się tak dalej składaniem tych transformacji szybko dojdziemy do wniosku, że nigdy nie wyjdziemy poza ogólną formułę dla transformacji w postaci prostego ułamka:

W(x) = (ax+b)/(cx+d).

Chcemy teraz sprawdzić, czy naszą transformację W z obrazka w istocie możemy przedstawić tą formułą. Innymi słowy, czy potrafimy dobrać a,b,c,d tak, by otrzymać nasze W? Mamy cztery niewiadome, potrzeba nam więc czterech równań, prawda? Takie równania z obrazka mamy, nawet pięć:

1. W(-9.25) = nieskończoność
2. W(0) = -2

3. W(6) = 3

4. W(8) = 4

5. W(11) = 5

Zatem, do algebry? Nie tak prędko. Z formuły na W w postaci ułamka widzimy bowiem, że jeśli a,b,c,d dają transformację W, to 2a,2b,2c,2d dają tą samą transformacje, bowiem dwójki z licznika i mianownika się uproszczą. Zatem nie da się z W(x) wyznaczyć a,b,c,d jednoznacznie. Najwyżej z dokładnością do wspólnego dla a,b,c,d skalującego czynnika. Tą niejednoznaczność należy czym prędzej usunąć! Inaczej nie wyliczymy naszych a,b,c,d. Moglibyśmy np. zażądać by zawsze a było jedynką. Jak nie jest jedynką, to licznik i mianownik podzielimy przez a i już przy x w liczniku będzie jedynka! Ale co, jeśli a w liczniku jest zerem, tak ja w transformacji (1) powyżej? Zatem nie jest to dobry pomysł. Dobrym pomysłem natomiast okazuje się dodatkowe zażądanie by wyznacznik ad-bc macierzy

[a b]
[c d]

był równy jedności. No, w najgorszym przypadku minus jedności. Dodajmy więc do naszego układu równań nowe równanie

6) ad – bc =1

i spróbujmy rozwiązać nasz układ równań. Mamy teraz jednak sześć równań na cztery niewiadome. Trochę jakby za dużo. Zrobimy więc tak: weźmiemy tylko trzy równania z naszej piątki, dodamy równanie 6) na wyznacznik, wyznaczymy z nich a,b,c,d i sprawdzimy, czy czwarte i piate spełnione jest automatycznie! Na warsztat weźmiemy równania 1), 2) i 4), zaś 3) i 5) potem sprawdzimy.

W(-9.25) = nieskończoność oznacza, że mianownik, cx+d musi się zerować dla x = -9.25. Czyli

c.(-9.25) + d = 0.

Stąd mamy od razu, że

d = 9.25c.

W(0) = -2 oznacza:

(a.0 +b)/(c.0+d) = -2

Czyli

b/d = -2,

zatem

b = -2d = -18.5c

Następnie weźmy równanie 4)

W(8) = 4 oznacza

(8a+b)/(8c+d) = 4.

Czyli

8a+b = 4(8c+d)=32c+4d

Podstawiając tu b i d wyrażone juz poprzednio przez c z łatwością znajdujemy

a = (32c+6d) = 10.9375 c

Podstawmy a,b,d to do naszego równania na wyznacznik:

ad-bc =1.

Po krótkich rachunkach z kalkulatorem dochodzimy do

119.672c² = 1

To już łatwo rozwiązać. Wybieramy rozwiązanie z c dodatnim, bowiem niejednoznaczność znaku zawsze pozostanie.

c=1/(sqrt(119.672)) = 0.0914122

gdzie sqrt oznacza pierwiastek kwadratowy. Teraz możemy już, z poprzednich wzorów, znaleźć a,b,c,d:

a = 10.9375 c = 0.99982

b = -18.5c = -1.69112

d = 9.25c = 0.845562

Jeśli więc się nie pomyliliśmy w rachunkach, to transformacja W z obrazka ma postać:

W(x) = (0.99982x-1.69112)/(0.0914122x+0.845562)

Sprawdzimy teraz, czy w istocie spełnione jest nasze równanie 3): W(6) = 3. Wychodzi nam

W(6) = 3.09016.

 

Nie najgorzej. A co z równaniem 5) – jest spełnione? Podstawiając dostajemy

W(11) = 5.02778.

Powinno wyjść 5. Nie będziemy się tym martwić, bowiem nasze dane wyjściowe były „na oko”, a na oko i tak nie potrafimy odróżnić dziesiątych części milimetra.

---

Jaki cel miała cała ta zabawa? Miała na celu oswojenie się z pewną grupa transformacji przeprowadzających prostą w prostą. Jest to początek tego, co matematycy nazywają „geometrią rzutową”. W istocie zajmowaliśmy się „rzutami”. Mamy w szczególności rzut równoległy – dający translację i rzut prostopadły dający inwersję. Wszystkie te rzuty, włączając w to rzuty ukośne, można zawrzeć w ogólnym wzorze transformacji ułamkowo liniowej:

W(x) = (ax+b)/(cx+d)

By usunąć niewygodną niejednoznaczność nałożyliśmy warunek na wyznacznik: ad-bc = 1. Wciąż mamy jednak mały problem z nieskończonością: a co, gdy mianownik się zeruje? Pisałem poprzednim razem, że problem zniknie, gdy prostą zamkniemy w okrąg, dodając punkt w nieskończoności. I to jest nasz cel. W drodze do tego celu mamy przed sobą parę przygód. Szkoda by było ich unikać.

Przygotowując powyższe czerpałem częściowo inspirację z książki Johna Stillwella „The Four Pillars of Geometry,” Springer 2005.

Cdn.