Rozmawialiśmy o błądzeniu losowym, o stanach czystych i o stanach mieszanych. Dziś trochę więcej ciekawostek o błądzeniu i krótka wizyta w krainie fraktali. Do samych kwantów wkrótce powrócimy.
Uwaga: O fraktalach wspominał, pisząc w sierpniu o fraktalnej kosmologii, już Eine w „Na tropie fraktalnego Wszechświata”, a o „kwantowych fraktalach” pisałem także, wszak bez wyjaśniania, i ja.
W poprzednim odcinku błądziliśmy po prostej. Na prostej nie bardzo można pobłądzić. Może właśnie dlatego żyjemy w przestrzeni trójwymiarowej? Choć już w przestrzeni o dwóch wymiarach zaczynają się dziać znacznie ciekawsze rzeczy (co nie oznacza bynajmniej, że wyczerpaliśmy już wszystko co ciekawego może się zdarzyć i w jednym wymiarze).
W jednym wymiarze mieliśmy do czynienia z losowym wyborem: krok w przód lub krok w tył. Innymi słowy obrót o 180 stopni. Na płaszczyźnie możemy zmieniać kierunek ruchu w sposób mniej trywialny. W następnych przykładach błądzenia losowego na płaszczyźnie (a ściśle mówiąc będziemy poruszać się w prostokącie, żeby nie wyjść za ekran!) będziemy nasz punkt błądzący poddawać transformacjom. Będą to albo obroty (względem początku płaskiego układu współrzędnych), albo ściśnięcia (co rozumiem przez ściśnięcie za chwilę wyjaśnię), albo też przesunięcia. Albo też złożenia tych trzech rodzajów transformacji.
Rozważmy punkt o współrzędnych (x,y), w „kartezjańskim układzie współrzędnych” (O Kartezjuszu pisałem tutaj) . Możemy go zbliżyć do początku układu współrzędnych dzieląc obydwie współrzędne przez dwa. Otrzymamy nowy punkt (x',y'):
x' = 0.5 x
y' = 0.5 y
Z drugiej strony możemy nasz punkt (x,y) przesunąć o wartość e w kierunku x oraz o wartość f w kierunku y. Otrzymamy wtedy nowy punkt:
x' = x+e
y' = y+f
Dlaczego użyłem liter e i f a nie, na przykład, a i b? Za chwilę się to wyjaśni, cierpliwości....
Możemy złożyć ze sobą te transformacje, najpierw ścisnąć o połowę, potem przesunąć. Wynikiem złożenia (wykonania jednej po drugiej) tych transformacji będzie:
x' = 0.5 x + e
y' = 0.5 x + f
Jest to szczególny przypadek ogólniejszej transformacji typu:
x' = a x + b y +e
y' = c x + d y +f
Tego typu transformacje matematycy nazywają afinicznymi, i tylko o takich transformacjach będziemy dziś mówić. Wygodnie jest użyć prostego kodu dla zapisu takiej transformacji. Będziemy ją zapisywać jako ciąg sześciu liczb (a,b,c,d,e,f). Tak więc transformacja pierwsza (ściśnięcie w tym samym stopniu w kierunku x co i y) ma kod (0.5,0,0,0.5,0,0) zaś transformacja druga (czyste przesunięcie) ma kod (1,0,0,1,e,f).
Teraz rozumiemy dlaczego użyłem poprzednio liter e i f dla przesunięcia. Bo pierwsze litery alfabetu a,b,c,d zarezerwowałem dla opisania transformacji bez przesunięcia (mówimy: jednorodnej), tzn. typu
x' = a x + b y
y' = c x + d y
Po tym wstępie przejdźmy do przykładów i zastosowań. Rozważymy na początek trzy różne transformacje, nazwiemy je odpowiednio T1,T2 i T3.
Oto one (używając naszego kodu)
T1 = (0.5,0,0,0.5,1.0,1.0)
T2 = (0.5,0,0,0.5,1.0,0.5)
T3 = (0.5,0,0,0.5,0.5,1.0)
Każda z nich jest złożeniem naszego ściśnięcia o połowę i przesunięcia. Ściśnięcia są te same dla wszystkich trzech przypadków, natomiast przesunięcia są różne. Dla T1 przesuwamy punkt o 1.0 w prawo i o 1.0 w górę. Dla T2 przesuwamy o 1.0 w prawo i o 0.5 w górę. Dla T3 zaś przesuwamy o 0.5 w prawo i o 1.0 w górę.
Przyjrzyjmy się co się stanie z wierzchołkiem kwadratu o boku równym 2, pomiędzy początkiem współrzędnych (x=0,y=0) a skrajnym punktem (x=2,y=2).
T1 przeprowadzi (x=2,y=2) w ten sam punkt. T2 przeprowadzi go w (x'=1.5,y'=2), zaś T3 w (x'=2,y'=1.5). Nietrudno się przekonać o tym, że jakikolwiek punkt z tego kwadratu nie weźmiemy, jego obraz pod wpływem każdej z tych transformacji będzie dalej leżał w tym kwadracie. To dobrze, bowiem za chwilę zaczniemy błądzić, startując z jakiegoś punktu w tym kwadracie i stosując losowo jedną z tych trzech transformacji. Ciekawe dokąd zajdziemy, nieprawdaż? Okazuje się, że więcej jest rzeczy ciekawych. Że ciekawy jest nie tyle kres naszej naszej podróży, ale także, a nawet bardziej, cała droga.
Jako, że mamy trzy transformacje, potrzebne nam będą trzy prawdopodobieństwa. Wybierzmy je każde równe 1/3. Nie ma monet o trzech równo prawdopodobnych stronach, możemy się jednak posłużyć kością do gry (byle nie zafałszowaną). Jeśli wyjdzie 1 lub 2, zastosujemy transformację T1, jeśli wyjdzie 3 lub 4, zastosujemy T2, jeśli zaś wyjdzie 5 lub 6 – zastosujemy T3, czemu nie.
Ile razy warto rzucić kością żeby coś ciekawego zaczęło być widać? Niestety WIELE razy. Jest to jeden z powodów dla których ta część naszej wiedzy zaczęła się na dobre rozwijać dopiero po pojawieniu się maszyn liczących. Na dzisiejszym PC-cie, kiedy program napisany jest w języku assembler, wyrzucenie kością 100 tysięcy twa krócej niż zmrużenie oka. Startujemy z dowolnie wybranego punktu początkowego we wnętrzu naszego kwadraty, rzucamy kością, stosujemy wylosowaną transformację, otrzymujemy nowy punkt. To nasz kolejny punkt startowy. Rzucamy kością, wybieramy transformację, stosujemy ją do punktu w którym się aktualnie znajdujemy i przeskakujemy do nowego punktu. Tak odmiana zabawa w klasy. Po 150 tysiącach kroków ślad naszej drogi ..... uwaga .....wygląda tak:

I kto by się spodziewał? Nazywa się to „dywanikiem Sierpińskiego”. Część czarna to część do której nigdy (no, ściślej, prawie nigdy, nie trafiamy)
Dlaczego jednak trzy transformacje? Czy dwie nie wystarczą? I owszem. Ciekawy ślad powstaje przy wyborze:
T1= (.824074, .281482, -.212346, .864198, -1.882290 ,-0.110607, .787473)
T2= ( .088272, .520988, -.463889, -.377778, 0.785360, 8.095795, .212527)
Uwaga: wprowadziliśmy tu (powszechnie stosowaną) nową umowę. Piszemy .824074 zamiast 0.824074 i dodaliśmy siódmą liczbę w nawiasie. Ta liczba to prawdopodobieństwo wybrania transformacji. Jak trzeba, zauważamy,
.787473 + .212527 = 1.0
A oto wynik błądzenia losowego z powyższymi dwiema transformacjami: Nazywa się to „krzywą smoka” (z ang. „dragon curve”)
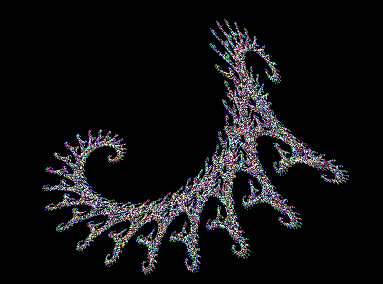
A co, jeśli sprytnie wybierzemy nie trzy i nie dwie, a cztery transformacje? Oczywiście pasjonaci wypróbowali tysiące, jeśli nie miliony możliwości w poszukiwania ciekawych transformacji. (Ściągnij program po nazwą „fractint”, jest też wiele innych o podobnych możliwościach) Wybór samych prawdopodobieństw nie ma przy tym wpływu na kształt a jedynie na cieniowanie tego kształtu.
Ciekawy wybór to:
T1 = ( 0, 0 , 0, .16 0, 0, .01)
T2 = ( .85,. 04, -.04, .85, 0, 1.6, .85)
T3 = ( .2, -.26, .23, .22, 0, 1.6, .07)
T4 = ( -.15,.28, .26, .24, 0 .44, .07)
lub zbliżony. Losując każdą z transformacji z prawdopodobieństwem ¼ otrzymujemy:

Czyli liść paproci (z ang. „fern”).
We wszystkich tych przypadkach wybór punktu startowego nie ma większego znaczenia. Postrzegany przez nas kształt drogi jest ten sam. Dlaczego? Matematycy wyjaśniają to używając terminów takich jak „chaos”i „atraktor” (ang. attractor) Nie będziemy w to teraz wchodzić.
Uwaga: Opisana przeze mnie metoda generowania obrazków atraktora różni się od tej opisanej w polskiej Wikipedii Przepis w Wikipedii operuje zbiorami punktów, ja operuję punktami. To prościej wyjaśnić.
I w ten oto sposób zajrzeliśmy do niezwykle bogatego świata fraktali. Tutaj się jednak z nim, póki co, rozstaniemy, bowiem wzywa nas przewodnik do dalszego zwiedzania świata osobliwości kwantowych
Na zakończenie mały żarcik. Przykład zjawiska częściowo losowego a częściowo deterministycznego. Włączony jest w to także czynnik „wolnej woli”. (Niezastąpiony komentator blogów, „tichy”, przypuszczalnie będzie tu miał coś więcej do powiedzenia). Oto migawka z rozkładu w świecie gości mojego blogu w ciągu ostatnich dwóch dni.
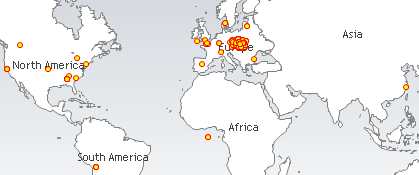
Wygląda na rozkład nieco chaotyczny, jednak widoczne są „centra przyciągające”. Interpretacja nie jest łatwa, bowiem odwiedzają mój blog zarówno ludzie, których to co piszę „przyciąga” jak i ci których to „odpycha” lub po prostu denerwuje :)

