Pod koniec poprzedniej notki otworzyliśmy okno, wpadła przez nie liczba zespolona i wcisnęła się do równania na funkcję przedstawiającą stan kwantowy:
ψ0,z(x) = c exp(-zx2/2)
I wszystko trzeba zaczynać od nowa. Przedtem funkcja była rzeczywista, teraz rzeczywistość utraciła. Przestała być dziecinnie niewinna.
Liczba zespolona z ma część rzeczywistą i część urojoną. Nazwijmy je u,v:
z = u+iv
gdzie u,v są rzeczywiste. Możemy zatem zapisać ψ0,z(x) tak
ψ0,z(x) = c exp(-(u+iv)x2/2) = c exp(-ux2/2) exp(-ivx2/2)
Chcemy c>0 dobrać tak, by ψ0,z(x) miało normę 1. Trzeba wycałkować po x
|ψ0,z(x)|2. Gdy obliczamy |ψ0,z(x)|2czynnik exp(-ivx2/2) nie gra roli, bo ma moduł 1.
|ψ0,z(x)|2= c2 exp(-ux2) .
By całka po x-ach była skończona, musi, ale to musi, być u dodatnie! Wtedy całkując po x (od -nieskończoności do plus nieskończoności) stwierdzamy, że by norma była równą 1 musimy wziąć c=(u/π)1/4. Więc tak zrobimy:
ψ0,z(x) = (u/π)1/4 exp(-zx2/2) , z =u+iv, u>0.
Gęstość prawdopodobieństwa rozkładu położeń, to
|ψ0,z(x)|2= (u/π)1/2 exp(-ux2)
Widzimy, że v tam w ogóle nie występuje. W notce poprzedniej, dla dziewiczej funkcji falowej mieliśmy u=1. A tu u może być dowolne, byle było dodatnie. Możemy zależność tej gęstości prawdopodobieństwa od zmiennej x i od parametru u namalować – tym razem w trzech wymiarach.
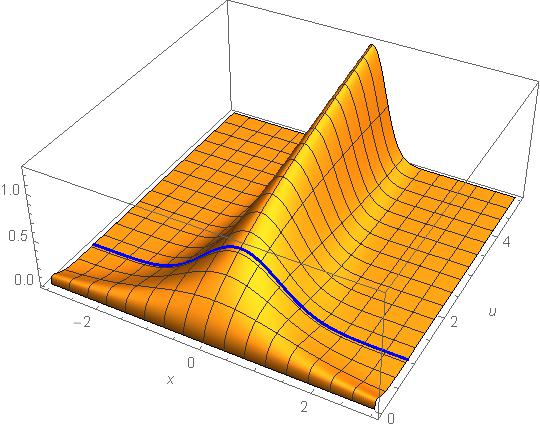
Niebieską linią namalowałem wykres z poprzedniej notki. Widzimy, że gdy u rośnie nasza kapeluszowata krzywa ulega ściskaniu z boków. Zaś gdy u zbliża się do zera, rozpłaszcza się.
Jak poprzednio możemy i teraz obliczyć standardowe odchylenie x-a. Ponieważ średnie x to 0, zatem obliczamy średnią z x2. W notce poprzedniej wychodziło 1/√ 2. Teraz wychodzi:
Δx = 1/√(2u)
Czym większe u, tym mniejsze rozmycie x-ów, jak to widać na rysunku.
A co z pędami? Trzeba zrobić transformatę Fouriera funkcji ψ0,z(x) . Daje się to wyrachować. Oto wynik:
Fψ0,z(p) = (u/π)1/4z-1/2exp (-p2/(2z)).
Możemy teraz obliczyć rozkład gęstości prawdopodobieństwa dla pędów, czyli |Fψ0,z(p)|2. Oto wynik:
|Fψ0,z(p)|2= (u/π)1/2(u2+v2)-1/2exp ( -p2u/(u2+v2) ).
W porównaniu z poprzednią notką mamy tu komplikacje. Trudno to namalować, bowiem mamy zależność od p i jeszcze od dwóch parametrów, u i v. Zrobiłem więc jedynie wykres dla v=1.
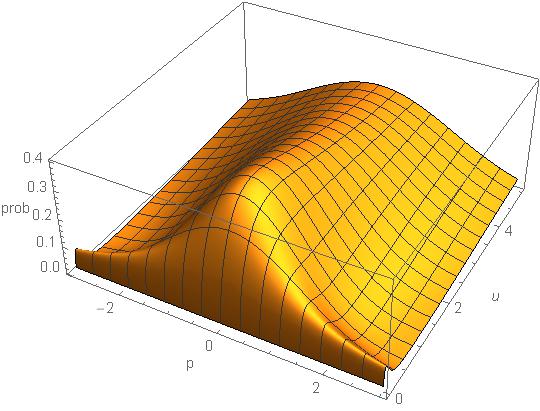
Dla pędów jest odwrotnie niż dla położeń: ze wzrostem u wykres się rozpłaszcza.
Możemy wyliczyć standardowe odchylenie dla pędów. Oto wynik:
Δp = (u2+v2)1/2/ √(2u)
Obliczamy iloczyn:
ΔxΔp = (1/2) √(1+v2/u2).
Widzimy, że iloczyn rozmyć położeń i pędów jest minimalny, równy 1/2, wtedy i tylko wtedy gdy v=0, czyli gdy z jest czysto rzeczywiste. Gdy z ma jakąś niezerową część urojoną, nasza paczka falowa, choć jakby gaussowska, jednak nie jest stanem o „minimalnej nieoznaczoności”.
Pozostaje nam do zrobienia analiza naszej paczki w przestrzeni fazowej, poprzez funkcję Wignera. Pojawią się wtedy elipsy. Ten przysmak pozostawmy jednak do następnej notki.










Komentarze