Kula i jej sferyczna powierzchnia to bodaj najbardziej symetryczne twory w przestrzeni. Kula ma środek – punkt centralny. Będziemy tę kulę wokół jej środka obracać. Chcemy jednak śledzić historię tego naszego działania. Przyczepmy więc do kuli trzy osie: Poobracajmy tę kulę trochę i zatrzymajmy się w jakimś końcowym położeniu.
Mając położenie początkowe i położenie końcowe okazuje się, że całą naszą historię obracania, jakkolwiek tego byśmy nie robili, daje się streścić w jednym stwierdzeniu:
Dokonaliśmy obrotu o pewien kąt wokół pewnej osi.
W tym streszczeniu cała historia naszego obracania znika. Można przecież obracać na różne sposoby, przechodząc przez różne konfiguracje pośrednie. Ale wynik końcowy daje się podsumować jak wyżej: obrót o jakiś jeden kąt wokół jednej osi. Te wyniki końcowe tworzą grupę: grupę trójwymiarowych obrotów. Czy to jednak wystarcza do opisania obrotów mających miejsce w rzeczywistości nas otaczającej? Czy materia nie ma jednak jakiejś formy pamięci? Czy tak całkiem nieważne są szczeble pośrednie? Czy nieważna jest historia? A jeśli jednak ważna, to na ile ważna? Ile z tej historii warto zatrzymać, a ile można pominąć jako mniej ważne, lub, dla praktycznych celów, w ogóle nieważne? Trudne to są sprawy i, jak sądzę, jesteśmy raczej na początku niż na końcu drogi. Współczesna fizyka jak tylko może stara się historię zbagatelizować. No, chyba, że zostanie przyparta do muru – wtedy ustępuje i jakoś się tam adaptuje. Gdy idzie o trójwymiarowe obroty do pewnego ustępstwa zmusiło nas tu odkrycie połówkowego spinu elektronu. Matematycznie pojęcie spinu ściśle wiąże się właśnie z historiami obrotów: mianowicie z drogami w tej grupie. Droga drodze nierówna. Wiąże się to też ze „splątaniem obiektu z otoczeniem.” Zajmiemy się tu przede wszystkim algebraiczną stroną problemu, ale tytułem wprowadzenia warto sobie obejrzeć filmik-animację „Aria na struny Diraca” na Youtube przedstawiającą w formie graficznej jeden z wyników takiego splatania – dopiero obrót o 720 stopni rozplątuje nici wiążące obiekt z otoczeniem. Obrót o 360 stopni nie wystarcza do przywrócenia stanu początkowego.
Przejdźmy zatem do szczegółów. Zajmujemy się grupą SL(2,C). Przypomnę definicję:
Definicja: SL(2,C) to grupa macierzy 2x2
[a b]
[c d]
o współczynnikach a,b,c,d zespolonych i o wyznaczniku ad-bc równym 1.
Podstawową dla nas będzie następująca własność:
Twierdzenie o rozkładzie biegunowym: Każdą macierz A z SL(2,C) można w sposób jednoznaczny rozłożyć na iloczyn
A = TU
gdzie T jest macierzą dodatnią o wyznaczniku 1, zaś U jest macierzą unitarną, też o wyznaczniku 1.
By to zrozumieć powinniśmy się zająć bliżej macierzami dodatnimi i macierzami unitarnymi. Zobaczymy, że macierze dodatnie są związane z relatywistycznymi „boostami”, po „polskiemu” „popychami”, zaś macierze unitarne opisują „zwykłe obroty”. No, nie takie całkiem zwykłe, bo te uwzględniają jakąś szczątkową pamięć o historii. Dojdziemy do tego.
Zaczniemy od macierzy unitarnych, bo te są wspólne dla fizyki relatywistycznej (po Einsteinie) i nierelatywistycznej (tej używanej już na długo przed Einsteinem).
Macierze unitarne o wyznaczniku 1 tworzą grupę. Grupę tę oznacza się symbolem SU(2) – Specjalna (bo o wyznaczniku 1) Unitarna grupa macierzy 2x2. Tę samą grupę oznacza się czasem symbolem Spin(3). Jest ona identyczna z grupą jednostkowych kwaternionów.
Czy można sobie SU(2) wyobrazić? Jaki ma „kształt”?
I można i nie można. Przede wszystkim można ją opisać. I tym opisem, a dalej, także wizualnym przedstawieniem jej struktury, się najpierw zajmiemy. Zasługuje na to.
Najpierw: co to znaczy „macierz unitarna”? W zapisie oznacza to, że
UU* = U*U = I
gdzie I jest macierzą jednostkową
[1 0]
[0 1]
U* jest tu macierzą hermitowsko sprzężoną do U. Jeśli U jest macierzą
[a b]
[c d]
to U* jest macierzą
[a* c*]
[b* d*]
gdzie gwiazdka przy liczbie zespolonej oznacza sprzężenie zespolone. Jeśli
a = x + iy
gdzie x,y są liczbami rzeczywistymi, to
a* = x – iy
Inżynier użyje tu „j” zamiast „i”, bo symbol „i” dla inżyniera jest często zarezerwowany dla czegoś innego.
Rozszyfrowując zapis UU* = I otrzymujemy:
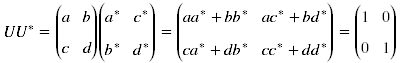
Porównując elementy macierzy widzimy, że
(1) aa* + bb* = 1
(2) ac* + bd* =0
(2') ca* + db* = 0
(3) cc* + dd* =1
Równania (2) i (2') zawierają tę samą treść: jedno otrzymuje się przez zespolone sprzężenie drugiego. Do tego dokładamy warunek na wyznacznik:
(4) ad – bc = 1.
Czy równania te można jakoś uprościć? Choćby częściowo je „rozwiązać”? A można. "To elementarne, drogi Watsonie!" - jakby powiedział Sherlock Holmes. Na przykład tak:
Bierzemy (4) i mnożymy obie strony przez a*:
ada* - bca* = a*
Mnożenie liczb zespolonych jest przemienne. Przestawiamy więc sobie jak nam wygodnie:
aa*d – bca* = a*
Z (2') widzimy, że ca* możemy zastąpić przez -db*. Więc zastępujemy:
aa*d + bdb* = a*
Przestawiamy jak nam wygodnie:
aa*d +bb*d = a*
Wyciągamy d za nawias:
(aa*+bb*)d = a*
Korzystamy z (1):
-
d = a*
Zatem d* = a.
Wracamy do (2) i podstawiamy d*=a,
ac* = - ba.
Jeśli a jest różne od zera, dzielimy przez a i dostajemy
c* = -b
lub, co na jedno wychodzi
c = -b*
A co jeśli a =0? Jeśli a=0 to z (1) dostajemy bb* = 1. Z (4) mamy wtedy
-bc = 1.
Mnożymy obie strony przez b* i mamy znowu ten sam wynik:
c = -b*.
Podsumowując:
Twierdzenie:
Każda macierz unitarna 2x2 o wyznaczniku 1 ma postać:
[ a b]
[-b* a*],
gdzie aa* + bb* =1. Łatwo sprawdzić, że, na odwrót, każda taka macierz jest unitarna.
Zapiszmy teraz a i b jako liczby zespolone z rzeczywistymi współczynnikami:
a = x1 + ix2, b = x3 + ix4.
Wtedy równanie
aa* + bb* =1
sprowadza się do
(x1)2 + (x2)2 +(x3)2 +(x4)2 =1
Jest to równanie sfery o promieniu równym 1 w czterowymiarowej przestrzeni euklidesowej. Każdemu punktowi tej sfery możemy przypisać macierz z grupy SU(2) i każdej macierzy z SU(2) odpowiada jeden punkt tej sfery.
Wniosek:Grupa SU(2) ma kształt trójwymiarowej sfery w czterowymiarowej przestrzeni.
No to już coś wiemy. Tylko czy to można narysować? Postaramy się narysować to co narysować się da. Ale to już w kolejnej notce. Podobnie jak powiązanie tej trójwymiarowej sfery z obrotami sfery dwuwymiarowej....

