Szczególna teoria względności opiera się na transformacjach Lorentza. Z angielskiej Wikipedii:
The Lorentz transformations relate the space-time coordinates, (which specify the position x, y, z and time t of an event) relative to a particular inertial frame of reference (the "rest system"), and the coordinates of the same event relative to another coordinate system moving in the positive x-direction at a constant speed v, relative to the rest system. It was devised as a theoretical transformation which makes the velocity of light invariant between different inertial frames. The coordinates of the event in this "moving system" are denoted x′, y′, z′ and t′. Before 1905, the rest system was identified with the "aether", the supposed medium which transmitted electro-magnetic waves, and the moving system was commonly identified with the earth as it moved through this medium. Early approximations of the transformation were published by Voigt (1887) and Lorentz (1895). They were completed by Larmor (1897, 1900) and Lorentz (1899, 1904) and were brought into their modern form by Poincaré (1905), who gave the transformation the name of Lorentz. Eventually, Einstein (1905) showed in the course of his development of special relativity, that this transformation concerns the nature of space and time.
Warto przetłumaczyć sobie na polski.
A tak oto wyglądały te transformacje w pracy Lorentza z roku 1904:

W roku 1919 Lorentz wydałzwięzłą ocenę roli i zasług Alberta Einsteina. Chwali tam Einsteina za jego odwagę myślenia. Podkreśla fakt, że Einstein rozstał się z „eterem”. Jednak jest zdania, że teoria Einsteina eterowi nie przeszkadza, sądzi, że fizyka do idei eteru wróci, tyle, że mocniejsza, bo będzie mogła z wkładu Einsteina zrobić użytek.
Więc, jak sądzę, warto się z transformacjami Lorentza bliżej zaznajomić. Dziś możemy to zrobić nieco inaczej niż robili to Lorentz, Poincare, Einstein i Minkowski. Możemy bowiem pobawić się macierzami. A jak macierze to i teoria kwantów gdzieś blisko, za rogiem. Zabawy starczy nam do nowego roku, a pewnie i na dłużej.
Zabieramy się do tego trochę nietypowo, bo interesuje nas przede wszystkim działanie transformacji Lorentza na sferę niebieską: jak zmienia się widok gwiazd gdy wsiadamy do pędzącego statku kosmicznego? Bo przecież jesteśmy na takim statku. Jego imię to Ziemia.
Notka dzisiejsza będzie robiła użytek z notek poprzednich. Wiemy, że z każdym punktem sfery niebieskiej widzianej „tu i teraz” możemy związać macierz hermitowską 2x2:
Ślad tej macierzy jest równy 1. Gdy (X,Y,Z) leżą na sferze jednostkowej
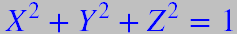
wtedy wyznacznik macierzy P jest równy zero. Na odwrót, każda macierz hermitowska 2x2 o wyznaczniku zero i śladzie równym 1 jest postaci jak wyżej. Nie jest to bynajmniej takie oczywiste, trzeba się troszeczkę napocić by to udowodnić.
Będziemy teraz działać na sferę macierzami zespolonymi o wyznaczniku 1. Czyli elementami z grupy SL(2,C). Jak to się robi? Zasada jest bardzo prosta. Wykonanie jednak żmudne. Do żmudnej roboty można zatrudnić komputer. (No, trzeba najpierw opanować jakiś język obliczeń symbolicznych, np. dostępny w sieci za darmo pakiet obliczeń symbolicznych Maxima spisuje się całkiem przyzwoicie. Można też użyć Reduce. Obydwa pakiety bazują na języku Lisp, ale znajomość Lisp'a nie jest konieczna. Ja Lispa nie znam a jakoś sobie z tymi pakietami potrafię dawać radę.). Podam więc samą zasadę i wynik obliczeń.
Od zespolonych macierzy z SL(2,C) do rzeczywistych macierzy transformacji Lorentza
W notce poprzedniej podałem formułę którą możemy związać z każdym punktem (T,X,Y,Z) czasoprzestrzeni macierz hermitowską 2x2
Ta (1/2) przed macierzą nie jest istotna. Można się umawiać i bez (1/2), wtedy (1/2) lub 2 wylezie gdzie indziej. Warto wprowadzić hermitowskie macierze bazowe, nazwę je tutaj s1,s2,s3,s4:
Wtedy naszą formułę na P(T,X,Y,Z) można zapisać jako:
Każdą macierz hermitowską 2x2 można w ten sposób zapisać. Z macierzy można odczytać współrzędne zdarzenia:
Zatem zdarzenia możemy kodować w macierzach i je z macierzy odkodowywać. Weźmy teraz jakąś dowolną macierz zespoloną A, też o dwóch wierszach i dwóch kolumnach. Możemy wtedy z macierzy P i macierzy A utworzyć nową macierz P' wykonując mnożenie macierzy:

Gwiazdka oznacza sprzężenie hermitowskie – transponujemy i sprzęgamy zespolenie (zmieniamy znak przy „i” na przeciwny). W szczególności P jest hermitowska, zatem P*=P. Teraz P' jest znowu hermitowska, co wynika z własności sprzężenia hermitowskiego:
Skoro tak, to macierz P' można rozłożyć na nasze macierze bazowe otrzymując w ten sposób współrzędne, nazwijmy je (T',X',Y',Z') nowego zdarzenia:
Jeśli A jest macierzą z grupy SL(2,C), czyli jeśli wyznacznik macierzy A jest równy 1 (choć nie tylko wtedy”) wtedy macierz P i P' mają ten sam wyznacznik:
Ale wyznacznik macierzy P jest równy podstawowemu niezmiennikowi transformacji Lorentza: interwałowi czasoprzestrzennemu:
wynika stąd, że nasza transformacja przeprowadzająca (T,X,Y,Z) w (T',X',Y'Z') zachowuje ten interwał – jest zatem transformacją Lorentza, bo tak właśnie w szczególnej teorii względności transformacje Lorentza są definiowane.
Pozostaje znaleźć w sposób jawny związek pomiędzy transformacją współrzędnych a współczynnikami macierzy A. I to jest robota nieco żmudna.
Zapiszmy macierz A w postaci
Współczynniki to liczby zespolone. Oto przykładowa taka macierz:
Tutaj a =0.1951i + 0.9138, b=0.3554i + 0.4823itd.
Transformacja Lorentza współrzędnych (X,Y,Z,T) w (X',Y',Z',T') jest transformacją liniową. Daje się więc zapisać jako działanie pewnej macierzy L na wektor o współrzędnych (X,Y,Z,T):
Trzeba teraz tylko wyrachować 16 współczynników L i wyrazić je przez a,b,c,d. Jak powiedział tak i zrobił. Oto wynik:
Trzeba to czytać tak: w tej ostatniej tabelce zamias L jest Lambda, pierwszy wskaźnik jest podniesiony do góry, nie ma tutaj to znaczenia, mam indeks 0 zamiast 4. Czasem wygodnie jest dla współrzędnej czasowej używać indeksu 0, czasem 4. Nie ma to znaczenia. W literaturze używa się zazwyczaj 0. Ale programista będzie wszędzie zamieniał 0 na 4. Te a,b,c,d z kreseczkami u góry to liczby zespolenie sprzężone z a,b,c,d. Na przykład gdy a =0.9138 + 0.1951i, to a z kreseczką jest równe 0.9138 – 0.1951i. To gotyckie R to „część rzeczywista” zaś gotyckie I to "część urojona" (współczynnik rzeczywisty przy "i") liczby zespolonej. I tyle.
Oczywiście, gdy sobie te formułki wyprowadziłem, wtedy zechciałem je sprawdzić czy nie zrobiłem jakiegoś błędu. Więc napisałem kod w Maximie, który generując losowo macierz A o wyznaczniku 1 wyliczył następnie według tych formuł L i sprawdził czy aby na pewno wyszła macierz transformacji Lorentza. No, wyszło, że jest. Prawdopodobieństwo zatem, że moje formułki zawierają błąd jest raczej znikome.
Teraz, skoro formułki mamy, możemy je zacząć dyskutować i stosować. Ale na to już dzisiejszej notce nie zostało miejsca. Zatem ciąg dalszy w notce kolejnej.

