Inwersja czyli nie tyle odwrócenie kota ogonem ile wywrócenie tego co wewnątrz na zewnątrz, i upchanie tego co było na zewnątrz do wnętrza. Czy to możliwe? Matematyka nie ma z tym problemów. Nam, zwykłym śmiertelnikom, w głowie się coś takiego mieści z wielkim trudem.
Inwersje są w samej rzeczy dość powszechne. Mamy kilka różnych rodzajów w muzyce. Jan Sebastian Bach był na przykład mistrzem od inwersji. Musiał je najwyraźniej lubić. Podobnie jak inne matematyczne igraszki. Mamy też inwersje w meteorologii – gdy następuje odwrócenie temperatur i wraz z wysokością temperatura lokalnie rośnie miast się obniżać. Prowadzi to do dość ciekawych efektów:
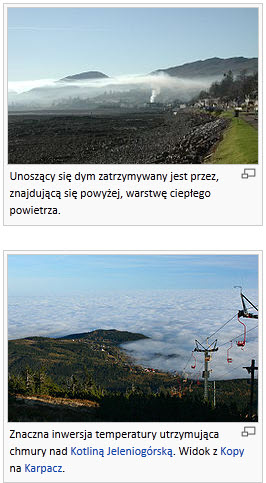
A ja chcę się dziś zająć inwersją dla liczb zespolonych, gdy na liczbach zespolonych dokonujemy transformacji
z → 1/z
Przypomnę z poprzedniej notki, że liczba zespolona z to nic innego aniżeli para liczb rzeczywistych z = (x,y). Możemy taką parę utożsamić z punktem na kartezjańskiej płaszczyźnie. Gdy chcemy punkt płaszczyzny zapisać jako liczbę zespoloną, zwykle piszemy
z = x+iy,
gdzie i2= -1.
Tak łatwiej pamiętać jak się mnoży i jak się dzieli liczby zespolone.
O każdej liczbie zespolonej z = x + iy można myśleć też jako o wektorze wychodzącym z początku układu współrzędnych O = (0,0) i kończącym się grotem w punkcie o współrzędnych (x,y) . Wektor taki ma określoną długość i określony kąt między nim a dodatnio skierowaną osią poziomą x-ów.
Długość tego wektora oznaczana jest zwykle przez |z| i nazywa się modułem lub wielkością absolutną liczby zespolonej z. Formuła na |z| wynika z prawa Pitagorasa:
|z|2 = x2 + y2
Kąt zaś nazywa się argumentem z, lub też jego fazą. Piszemy czasem Arg(z). Są przy tym możliwe dwie umowy. Jedni uważają, że Arg(z) powinien się zmieniać od 0 do 2 pi, inni zaś, że od -pi do pi. Trzeba więc uważać przy czytaniu tekstów jaką umowę dany autor stosuje.
Mnożenie licz zespolonych ma prostą interpretację geometryczną: mając liczbę zespoloną z mnożymy ją prze liczbę zespoloną u: długość wektora zu to iloczyn długości wektora z i wektora u.
Jeśli więc |u| = 2, to wektor zu będzie dwa razy dłuższy niż wektor z. Natomiast fazy przy mnożeniu się dodają (modulo 2 pi). Jeśli więc u tworzy z osią x kąt phi, to o kąt phi (przeciwnie do kierunku ruchu wskazówek zegara) należy z obrócić. Czyli: pomnożyć z przez u, to z przeskalować i obrócić (albo obrócić i przeskalować - kolejność nie ma w tym przypadku znaczenia).
Uwaga: w wersji pierwotnej notki dokonałem inwersji i napisałem błędnie "zgodnie z kierunkiem ruchu"
Stąd też wynika interpretacja dzielenia przez liczbę zespoloną: przeskalować i obrócić, tyle że w przeciwnym kierunku, a przy skalowaniu dzielimy a nie mnożymy.
Jaka stąd wynika interpretacja transformacji z → 1/z?
Proste: bierzemy z i odbijamy względem osi x (argument z zmienia się wtedy na przeciwny). Następnie skracamy lub wydłużamy. Gdy |z| = 10, to |1/z|=1/10, gdy |z| = 1/10 to |1/z| = 10. Co było bliska zera – ucieka daleko. Co było daleko, zbliża się do zera. Takie wywrócenie i przekręcenie.
Oczywiście z = 1 przy takiej transformacji nie ulega zmianie. Podobnie jak z = -1.
Trochę nam to może estetycznie nie grać. W życiu codziennym częściej obracamy się na pięcie wokół osi pionowej, niż stajemy na głowie.W związku z tym umówmy się, że dla nas inwersją będzie transformacja S definiowana jako
S(z) = -1/z
Dodaliśmy "–" przed 1/z. Teraz, przy tak zdefiniowanej inwersji, które to punkty są stałe?
S(z) = z
Oznacza to
-1/z = z
Czyli
z2 = -1
A to ma dwa rozwiązania: z = +i, z = -i. To są dwa punkty na osi pionowej y:
(0,1) oraz (0,-1)
Nasza inwersja z → S(z) to odbicie względem osi pionowej i przeskalowanie (odwrócenie długości).
Zauważmy, że dwukrotnie zastosowana inwersja przywraca stan oryginalny:
S(S(z)) = z
dla każdego z. Co możemy zapisać jako S2 = 1 (przekształcenie identycznościowe)
A teraz zobaczmy jak to wygląda na przykładzie mapy Polski. Nasza mapka wygląda tak:
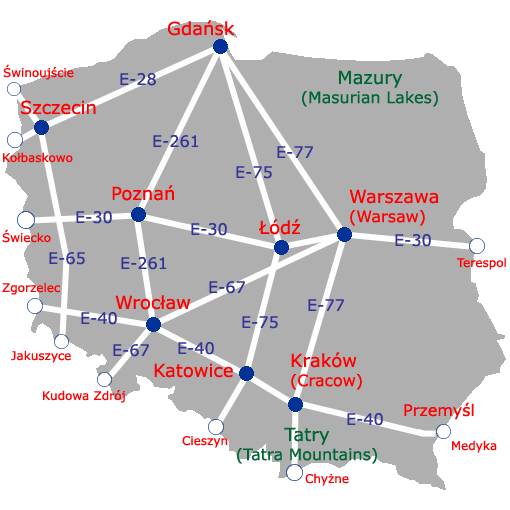
Łódź jest w pobliżu środka czyli punktu (0,0) – powinna więc uciec gdzieś daleko. A peryferie winny wejść do środka. Całą mapkę potraktowałem jako kwadrat gdzie x i y zmieniają się od -1 do 1 – żeby było symetrycznie. Wynik zaś przedstawię w kwadracie -10 do 10. Oto ten wynik:
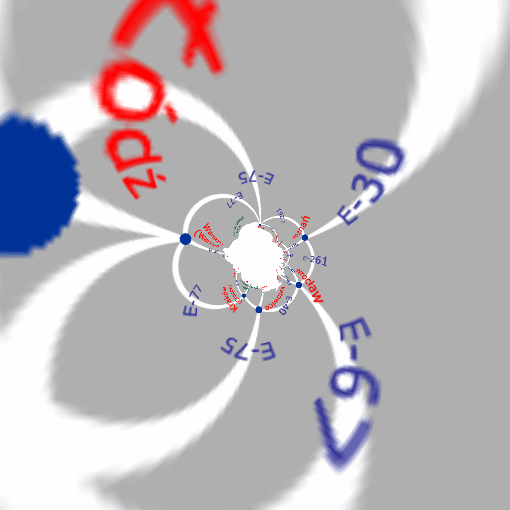
Cieszy mnie to, że Wrocław, po inwersji, prezentuje się całkiem nieźle!
W przyszłej notce wprowadzimy jeszcze jedną ciekawą transformację na liczbach zespolonych. Wraz z inwersją te dwie transformacje generować będą całą grupę SL(2,Z) – a stąd już do paradoksu typu Hilberta-Banacha-Tarskiego będzie niedaleko.

