„Czar, doskonałość, symetria jak w greckiej rzeźbie.”
Margaret Mitchell - Przeminęło z wiatrem
„Asymetrie mają zawsze jakiś powód (...). To asymetrie czynią nasze życie w ogóle możliwym. Różnice płci. Bieg czasu zawsze w jednym kierunku. Asymetrie zawsze mają jakiś powód i jakieś znaczenie.”
Peter Stamm - Agnes
W bieżącej serii notek zajmuję się najprostszą geometrią skończoną – geometrią płaszczyzny rzutowej Fano. Geometria ta zwykle ilustrowana jest takim obrazkiem:
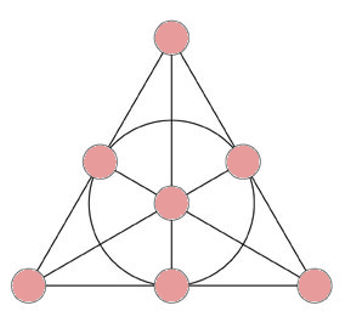
Możemy się tam z łatwością doliczyć siedmiu linii (jedna kolista) i siedmiu punktów. I to jest cały nasz świat. Literatura w języku polskim dotycząca tego ważnego tematu jest niezmiernie uboga. Szukając w polskim Google natrafiam niemal od początku na moje własne notki. Tę lukę zatem wypełniam. Interesują nas aktualnie symetrie tej geometrii. Powyższy obrazek nie zdaje dobrze sprawy z symetrii. Widać jakby jeden punkt wyróżniony – centrum trójkąta, także jedną wyraźnie wyróżnioną linię – tę kolistą. A przecież to wyróżnienie jest tylko własnością modelu, własnością naszego sposobu przedstawiania tej geometrii, nie zaś własnością „geometrii samej”. Aby to dobrze zrozumieć trzeba jednak najpierw zdefiniować „geometrię samą”. Można to robić na kilka sposobów – te okazują się równoważne. A co to znaczy „równoważne”? Znaczy to, nie mniej ni więcej, że te różne sposoby prowadzą do tej samej grupy symetrii.
Pierwszy sposób to sposób aksjomatyczny – poprzez opisanie własności punktów i linii. Drugi sposób, to przedstawienie geometrii Fano jako geometrii rzutowej. I tym się ostatnio zajmujemy. Mamy więc sześcian jednostkowy, ten ma osiem wierzchołków. Jeden z tych wierzchołków umieszczamy w początku układu współrzędnych O=(0,0,0). Wtedy każdy z pozostałych siedmiu wierzchołków P definiuje linię łączącą O z P. Te linie to punkty naszej geometrii. Badając tę geometrię posługujemy się jedynie arytmetyką liczbami 0 i 1 z regułą 1+1=0 – czyli „modulo 2”. Pełną grupa G symetrii naszej geometrii jest wtedy grupa macierzy odwracalnych o trzech wierszach i trzech kolumnach, z zerami i jedynkami w komórkach. Grupa ta, oznaczana symbolem GL(3,2) ma 168 elementów.
Każda z tych symetrii permutuje (każda inaczej) siedem różnych od O wierzchołków naszej kostki. Symetrie siedmiokrotne, a jest ich 48, nie zostawiają żadnego wierzchołka w spokoju. Orbity tej grupy tworzą zygzaki obiegające na 48 sposobów wszystkie siedem wierzchołków.
W ostatniej notce zainteresowaliśmy się jednak tymi symetriami, które nie ruszają jednego z wierzchołków, mianowicie wierzchołka (0,0,1). Bjab jednak, w swoim komentarzu, poprosił bym raczej wyróżnił wierzchołek (1,1,1), który wydaje się być bardziej symetryczny. Życzeniu temu spełniam więc teraz zadość.
Badamy więc te symetrie, które punku (1,1,1) nie ruszają. Ponieważ nie ruszany jest punkt (0,0,0), zatem symetrie te mogą co najwyżej ruszać jakoś pozostałe sześć punktów. Podgrupa H grupy G=GL(3,2) złożona jest z 24 symetrii. Jako, że nasza grupa jest grupą o skończonej liczbie elementów, każda symetria ma określony „rząd n”: gdy powtórzymy działanie tej symetrii n razy – wtedy tak jakbyśmy w ogóle nie działali. Zatem g....g (n razy) = e – symetria identycznościowa.
W podgrupie H pojawiają się symetrie o rzędzie 1,2,3,4. I to wszystko. Przy tym rząd 1 ma jedynie identyczność (jedynka) e grupy. Ta nie będzie niczego ruszać. A co robią pozostałe trzy elementy?
By odpowiedzieć na to pytanie wyrysowałem orbity każdego z elementów g podgrupy H. Biorę w tym celu jeden z siedmiu (różnych od O) wierzchołków sześcianu i działam nań kolejno potęgami symetrii g. Jeśli g ma rząd n, wtedy wystarczy, że podziałam n razy – wtedy wrócę na pewno do punktu wyjścia. Otrzymuję jedną z orbit symetrii g. Teraz biorę któryś z pozostałych punktów, który do już wyrysowanej orbity nie należy – i czynie to samo. I tak czynię aż wyczerpię wszystkie wierzchołki. Punktu (1,1,1) oczywiście nie będzie ruszać żadna symetria z H – tak bowiem H zostało zdefiniowane. Orbitą punktu (1,1,1) jest on sam.
A oto wygenerowany przeze mnie komputerowo obrazek orbit dla każdego 24 elementów podgrupy H:
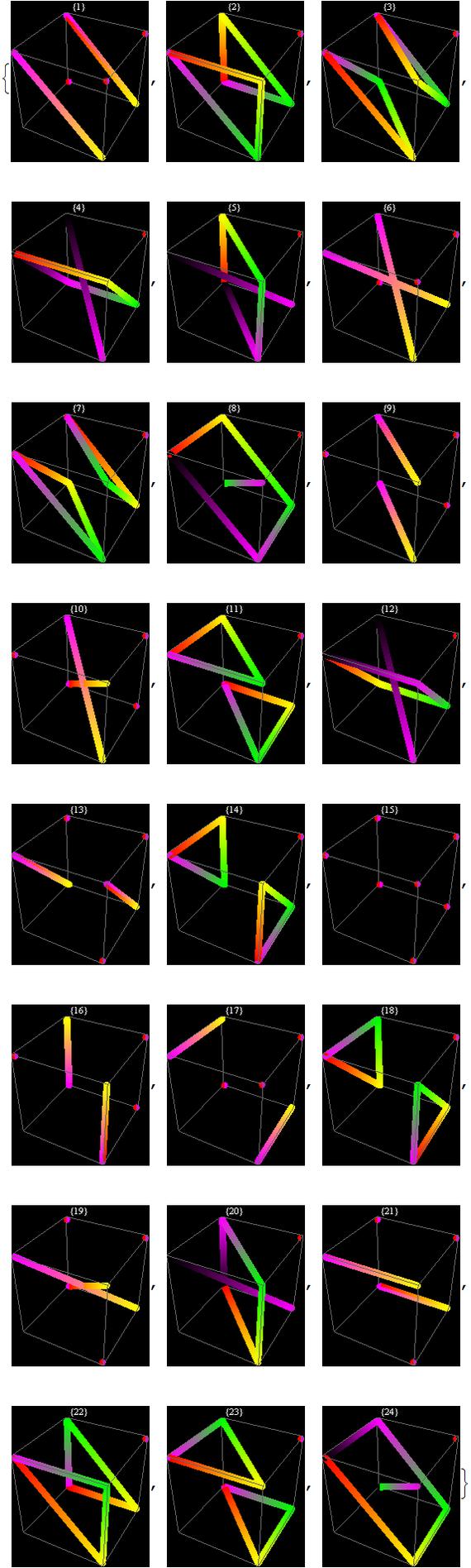
W moim programie dla każdej z orbit startowałem od jakiegoś punktu. Kierunek obiegu zaczyna się zawsze od koloru czerwonego, poprzez żółty, niebieski …. Jednak punkt startowy nie jest ważny – bo każda orbita cyklem. Możemy wystartować z dowolnego punktu takiego cyklu i orbita się od tego nie zmieni!
Zadanie dla Czytelników: patrząc na orbity odczytać, które z symetrii (i ile ich jest) są dwukrotne, które trzykrotne, a które czterokrotne? Można też wypatrzyć tę symetrię trywialną – jednokrotną.

