Zdarza się czasem, że przychodzi nam, ni z tego ni z owego, myśl do głowy: „to już było”. Już kiedyś się z czymś taki spotkali. Tak jakby rzeczywistość była, w pewnym stopniu, cykliczna. Czy tak jest faktycznie? Czy też tak się nam tylko wydaje?
Cyklami zajmę się w dzisiejszej notce – tej z cyklu „grupa 168”. Bo. Moim zdaniem, najlepiej uczyć się (i bawić zarazem) najlepiej na konkretnych przykładach. A czego nauczyliśmy się na jednym przykładzie, to, po odpowiednich zmianach, możemy stosować do innych przypadków.
W niniejszym cyklu przyglądamy się najprostszej ze skończonych geometrii – geometrii płaszczyzny rzutowej Fano. A cykl ten narodził się dzięki mojej notce „Geometryczne śmieciowe DNA” a także dzięki pytaniom moich Czytelników na którezareagowałem wtedy np. tak:
@Bjab
"Co to są te grupy przekształceń?"
O tym trzeba by pisać więcej.
,,,,
No wiec piszę – więcej.
Geometrię Fano modelowaliśmy na kilka sposobów:
-
A to jako model o symetrii trójkątnej:
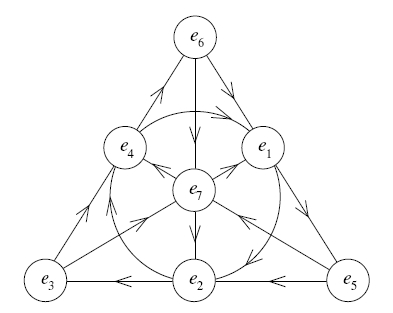
-
A to jako model czworościenny
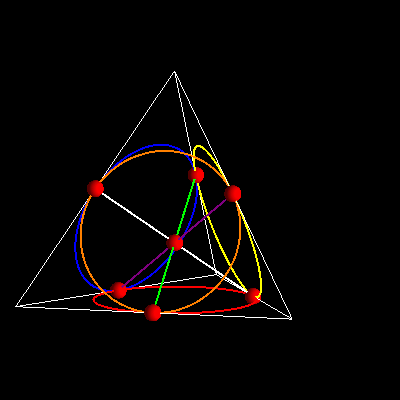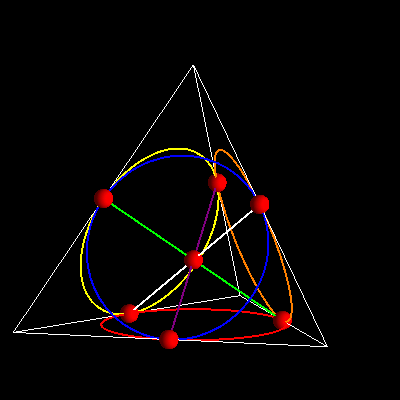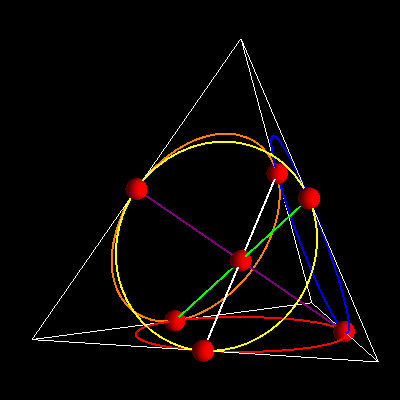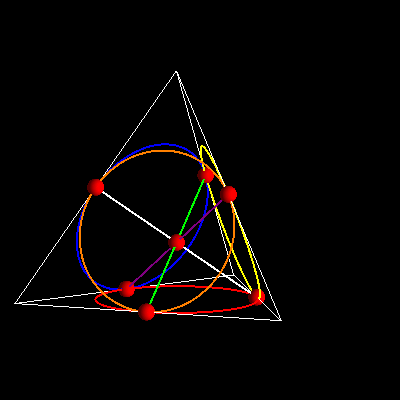
-
A to jako siedmiokrotny
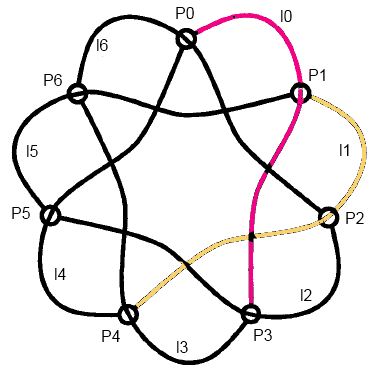
W końcu przedstawiliśmy tę geometrię jako zbiór linii i płaszczyzn w trójwymiarowej przestrzeni zero-jedynkowej i doliczyliśmy się dzięki temu, bez bólu, 168 elementów symetrii tej geometrii. Symetrie te tworzą grupę. Można je ze sobą składać: wykonanie dwóch transformacji z tej 168-elementowej grupy grupy daje znów transformację z tej grupy. Mamy więc tabliczkę mnożenia, i nawet ją, w poprzedniej notce, jakoś tam tam, w stylu łowickim, namalowaliśmy.
Przyjrzyjmy się dziś bliżej tej naszej grupie – tym razem pod kątem właśnie cykliczności.
Co będzie gdy weźmiemy jakiś jeden element z naszej grupy, powiedzmy g, jakąś jedną transformację symetrii, i zaczniemy ją powtarzać. Wiemy, z poprzednich notek, że nasza transformacja może być przedstawiona jako tabelka (macierz) o trzech wierszach i trzech kolumnach, z zerami i jedynkami w klatkach (a klatek jest 3x3 = 9). Składaniu transformacji odpowiada mnożenie macierzy. Powtarzanie jednej transformacji, raz po raz, to potęgowanie macierzy.
Przyglądamy się zatem ciągowi:
g, g2, g3, g4,....
Operując na macierzach musimy wszakże pamiętać o tym, że pracujemy z arytmetyką zero-jedynkową, gdzie obowiązuje prawo 1+1=0.
Biorąc kolejne potęgi jednego elementu będziemy otrzymać nowe elementy. Ale czy zawsze „nowe”?
Nasza grupa jest skończona. Ma 168 elementów. Jeśli więc weźmiemy, jedna po drugiej, powiedzmy 169 potęg g, g2, g3, g4,....,g169, to któreś dwie potęgi muszą być identyczne! Będziemy mieć więc sytuację, że istnieją liczby całkowite k oraz l,l większe lub równe k takie, że
gl = gk
Ale nasze transformacje są odwracalne. Możemy więc nasze równanie powyżej pomnożyć przez g-k by otrzymać
gl-k= e
gdzie e jest transformacją identycznościową, przedstawianą jako macierz jednostkowa. Mamy więc cykl.
Dla każdego elementu g naszej grupy istnieje więc liczba całkowita n taka, że gn= e. Najmniejsza z liczb n o tej własności nazwijmy „rzędem” tego elementu. To rozmiar cyklu tego elementu.
Każda z naszych 168 symetrii ma więc swój rząd. Nie powinno nas to zaskakiwać. Jeśli np. rozważamy symetrię obrotu o 120 stopni, ewidentną dla modelu trójkątnego, to jasne, że ta symetria ma rząd 3. Dlaczego? Bo wykonanie po sobie trzech kolejnych o 120 stopni daje obrót o 360 stopni – transformację identycznościową.
Z rozważań w poprzednich notkach wiemy więc, że badając rzędy kolejnych 168 elementów naszej grupy natrafimy na elementy rzędu 2 (odbicia lustrzane), elementy rzędu 3 (jak obrót o 120 stopni), oraz elementy rzędu 7 (obrót o 360/7 stopni w modelu o symetrii siedmiokrotnej).
Ale czy pojawią się też elementy o rzędzie innym?
Zatem pytanie: jakiej długości cykle występują w naszej grupie? No i kolejne pytanie: dla każdej długości cyklu – ile jest w naszej grupie elementów o cyklu tej długości?
Są to pytania natury demograficznej odnośnie naszego 168-elementowego społeczeństwa.
Można na nie znaleźć odpowiedź, na przykład posługując się programem Maxima, który to program prezentowałem w poprzednich notkach.
Czy ktoś będzie w stanie na te pytania znaleźć odpowiedź? Choćby i częściowo zgadując ...

