Nie wiem kto i kiedy wymyślił gry karciane. Różne gry mają różne zasady. Wspólną częścią wszystkich tych gier jest ceremonia „tasowania”. Jedni tasują tak, inni inaczej. Są sposoby tasowania wymagające nie byle jakiej zręczności i wprawy. W czasie tasowania zmieniamy kolejność ustawienia kart. Dzisiaj będziemy tasować geometrię.
Początkowo miałem większe ambicje, chciałem tasować geometrię Fano, tą o siedmiu punktach i siedmiu liniach, o której piszę w obecnym cyklu notek. Jednak po przespanej nocy zmieniłem pierwotny plan. Postanowiłem zacząć od prostszego przypadku, niemal banalnego. A jednak dokładne przeanalizowanie tego właśnie przypadku pozwoli nam na uniknięcie wpadek w przypadkach bardziej złożonych.
Zacznę więc od geometrii banalnej, „trójkątnej”, o trzech liniach i trzech punktach. Jak na tym obrazku:
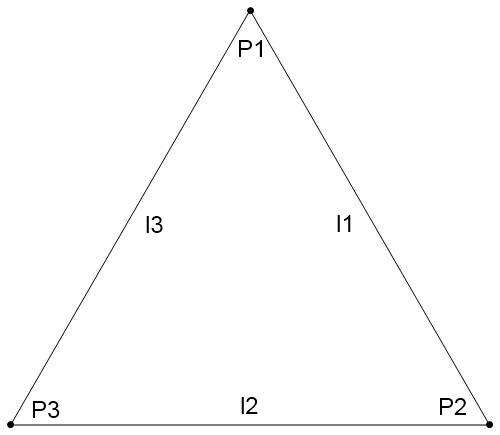
Chcemy znaleźć wszystkie różne „transformacje symetrii” tej geometrii. Ale co to znaczy „transformacja symetrii”? Intuicyjnie czujemy, że gdy obrócimy nasz trójkąt, z ponumerowanymi punktami i liniami, o 120 stopni – nic się w geometrii nie zmieni. Zmieni się jedynie nasza własna perspektywa.
Podobnie możemy zamienić miejscami punkty P2 i P3. Ale jeśli chcemy by relacje między punktami i liniami nie uległy zmianie, musimy też jednocześnie zamienić miejscami linie l1 i l3.
Ile jest więc różnych tasowań punktów i linii, tasowań, które pozostawiają niezmienionymi relacje pomiędzy naszymi ponumerowanymi punktami i liniami? Można zgadywać, ale można też wyliczyć. I dzisiaj chcę pokazać jak to można wyliczyć.
Na czym polega tasowanie geometrii? Cóż, możemy niezależnie tasować punkty i tasować linie. Ile jest tasowań punktów? Mamy punkty P1,P2,P3. Punkt P1 może przy tasowaniu przejść w jeden z trzech punktów: P1,P2,P3. Na przykład w P2. Jak już przejdzie i się tam usadowi, wtedy punkt P2 może przejść w jeden z dwóch wolnych punktów P1,P3. Powiedzmy w P3. Wtedy P3 już nie ma wyboru, musi przejść w nieobsadzony P1. Tasowań punktów jest więc 3x2x1=6. Ogólnie, gdym mamy n punktów, możemy przetasować je na nx(n-1)x(n-2)x(n-3)x....x2x1=n! sposobów. Dla trzech punktów mamy 3!=6. Dla siedmiu punktów będziemy mieć 7!=7x6x5x4x3x2x1=5040 sposobów.
Niezależnie możemy tasować linie, też trzy, zatem możemy je przetasować również na sześć sposobów. Gdy będziemy tasować i punkty i linie, wtedy będziemy mieć 6x6=36 różnych tasowań geometrii trójkątnej.
Ile z tych trzydziestu sześciu tasowań nie zmieni relacji pomiędzy liniami i punktami?
Można to liczyć na papierze, bo liczba 36 nie jest przerażająca. Ale gdy przyjdzie do geometrii Fano, wtedy będziemy mieć 5040x5040=25401600 tasowań (ponad 25 milionów!) i tego liczyć nam się już nie będzie chciało. Raczej zechcemy skorzystać z usług naszego współczesnego pomocnika – komputera. Warto będzie wtedy popracować nad przedstawieniem naszego zadania w języku zrozumiałym dla maszyny liczącej.
Najpierw musimy zakodować naszą geometrię. Idzie o zakodowanie relacji pomiędzy liniami i punktami. Zrobimy to w postaci tabelki o trzech wierszach (przedstawiających punkty) i trzech kolumnach (przedstawiających linie). Tabelka kodująca naszą trójkątną geometrię wygląda tak:
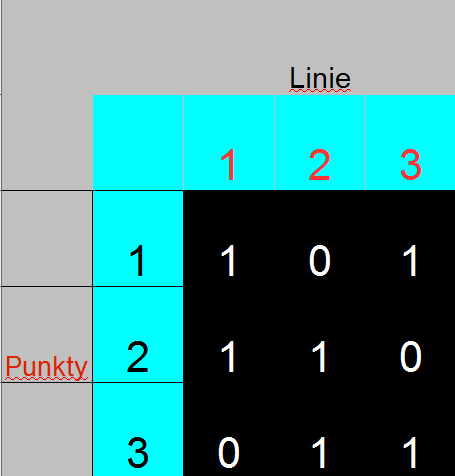
W kolumnie 1, przedstawiającej linię l1, wpisałem dwie jedynki dla punktów odpowiednio P1 i P2 leżących na tej linii, oraz 0 dla punktu P3, który na tej linii nie leży. Podobnie z pozostałymi dwoma liniami. Otrzymałem tabelkę kwadratową 3x3 z zerami i jedynkami. Nazywa się to po angielsku „incidence matrix”. Po polsku nie wiem jak to się nazywa. Będę używał zwrotu „macierz incydencji”.
Geometrię mamy zakodowaną.
Teraz jak opisać tasowania punktów i linii? Dokonuje się tego przy użyciu macierzy (tabelek) tasujących. Macierz tasująca to macierz, która w każdym wierszu ma tylko jedną jedynkę, pozostałe zera. I podobnie w każdej kolumnie.
Macierz tasująca to macierz, która w każdym wierszu ma tylko jedną jedynkę, pozostałe zera. I podobnie w każdej kolumnie.
Dla przykładu macierz P
[0 1 0]
P = [1 0 0]
[0 0 1]
jest taką macierzą. A jak ona tasuje? Tu dobrze jest nauczyć się mnożenia macierzy. Albo, jeśli ktoś uważa to za trudne, można zlecić mnożenie macierzy komputerowi, bo na przykład OpenOffice lub Excel to potrafi robić na swoich arkuszach kalkulacyjnych. Instrukcję jak mnożyć macierze w arkuszu kalkulacyjnym można znaleźć np. tutaj: Mnożenie macierzy. Instrukcja nie jest tak całkiem, całkiem jasna, ale po małym ćwiczonku można to opanować. Ja przynajmniej, który zbyt bystry nie jestem, opanowałem to w parę minut.
Dla prób i zorientowania się co nasze tasujące macierze robią, utwórzmy macierz próbną M:
[1 2 3]
M= [4 5 6]
[7 8 9]
A teraz każmy arkuszowi kalkulacyjnemu utworzyć iloczyny PM i MP. Zrobiłem sobie to ćwiczonko i wyniki były takie:
Mnożąc M przez P z lewej strony przestawiamy wiersze macierzy M. Mnożąc M przez P z prawej strony – przestawiamy kolumny macierzy M.
No i to już wszystko co nam potrzeba. Teraz trzeba wygenerować macierze tasujące. W naszym przypadku jest ich sześć. Można je wypisać ręcznie. Można zaprogramować jakoś komputer – zależy od tego kto jakim językiem komputerowym się posługuje. Zapewne można to zlecić arkuszowi kalkulacyjnemu.
Uwaga: Ja w Visual Basic for Applications dobry nie jestem, używam z reguły programu Mathematica, który ma dość rozbudowany język dla takich celów. W języku Mathematica mogę wygenerować macierze tasujące jedną linijką dla dowolnego n używając funkcji:
f[n_]:=Map[#//MatrixForm&,Map[SparseArray[{i_,i_}-> 1,{n,n}][[#]]&,Permutations[Array[#&,n]]]]
Wywołując teraz f[3] otrzymuję sześć macierzy tasujących:
Moja funkcja f generuje macierze tasujące w formie przyjemnej dla oka, jednak do obliczeń potrzebna mi inna forma. Tworzę więc tabelkę rozrzedzonych macierzy komendą
Teraz pozostaje jedynie wymnożenie naszej macierzy incydencji M przez macierze tasujące P, z lewej i z prawej i zobaczenie kiedy macierz M się przy takim mnożeniu nie zmienia. Innymi słowy, jeśli nasze sześć macierzy tasujących oznaczę przez P(i), i=1,2,3,4,5,6, to chcę znaleźć te pary (i,j) przy których
P(i)MP(j) = M
Zrobiłem to, i każdy kto sprawny w jakimś języku komputerowym może to sprawdzić, a wynik (przy mojej numeracji macierzy tasujących) jest taki:
(1,1),(2,6),(3,2),(4,5),(5,4),(6,3)
Odpowiada to takim parom macierzy P:
1)
{1, 0, 0},
{0, 1, 0},
{0, 0, 1}
{1, 0, 0},
{0, 1, 0},
{0, 0, 1}
Ta nic nie robi – punkty i linie pozostają na swoich miejscach
2)
{1, 0, 0},
{0, 0, 1},
{0, 1, 0}
{0, 0, 1},
{0, 1, 0},
{1, 0, 0}
Czytamy: punkt pierwszy pozostaje na miejscu, punkty 2 i 3 zamieniają się miejscami, l1 przechodzi w l3, l2 zostaje na miejscu, l3 przechodzi w l1. Ach, rozpoznajemy: to odbicie całego trójkąta względem osi pionowej!
I tak możemy zinterpretować wszystkie sześć transformacji.
Teraz już wiemy z całą pewnością: grupa symetrii naszej trójpunktowej geometrii jest z całą pewnością sześcioelementowa! W naiwnych rachunkach z poprzednich notek - 3x2 = 6 (trzy obroty razy dwa odbicia) nie przegapiliśmy niczego. Komputer nam tego dowiódł.
W następnej notce zastosuję tą samą metodę do geometrii Fano. Tym razem komputer będzie musiał sprawdzić ponad dwadzieścia pięć milionów równań P(i)MP(j)=M. Zajmuje to, na moim komputerze, około pięciu minut. W wyniku otrzymuję 168 par (i,j) które przedstawiają wszystkie możliwe symetrie geometrii Fano.No i zahaczymy nieco o mistykę - przecież mamy lato!

