W poprzednich notkach zobaczyliśmy trzy modele jednej geometrii – słynnej geometrii Fano, z siedmioma punktami i siedmioma liniami. Za siedmioma górami, za siedmioma rzekami żyła-była sobie … geometria płaszczyzny rzutowej Fano.
Model pierwszy, niejako standardowy, to model o symetrii trójkąta równobocznego:
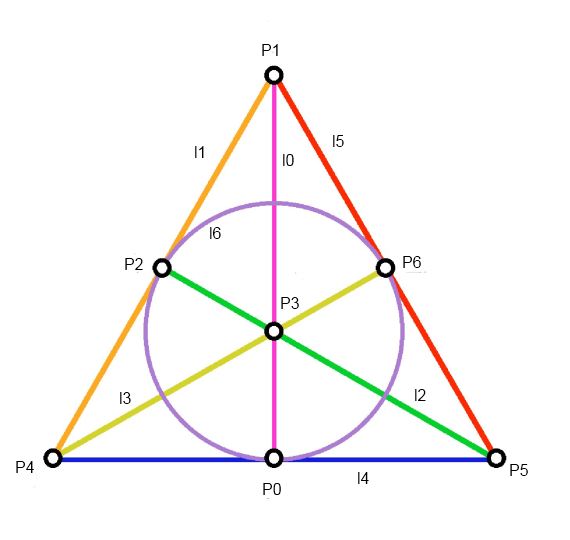
Ani kolorki, ani numerki do samej geometrii nie należą. To dodatek od nas, by łatwiej było prowadzić buchalterię.
Model drugi – to model o symetrii siedmiokrotnej:
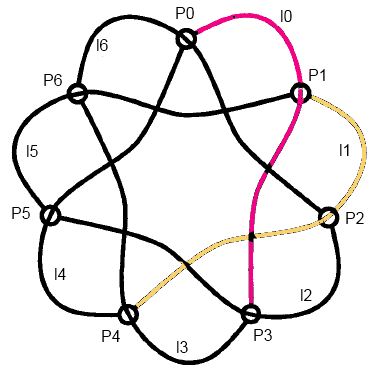
I znów numerki punktów i linii do geometrii nie należą. Umieściłem je po to, byśmy mogli o liniach i punktach rozmawiać. Punkt P1 nie jest ani lepszy ani gorszy od punktu P3. Geometria nie wyróżnia żadnego punktu ani żadnej linii. Wyróżnić coś może jedynie nasza koncentracja świadomości..
Wreszcie model trzeci – to model o symetrii czworościanu foremnego:
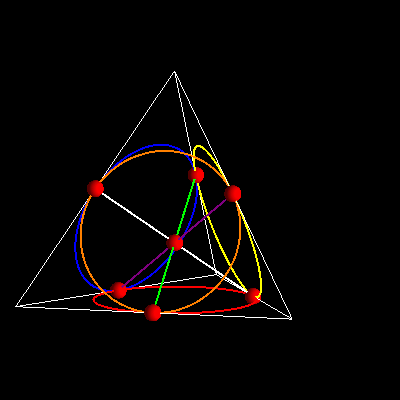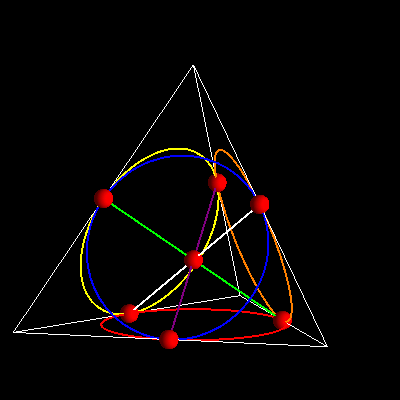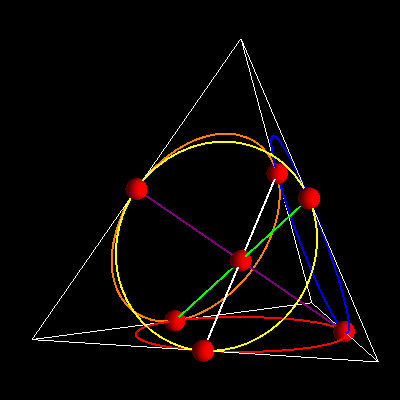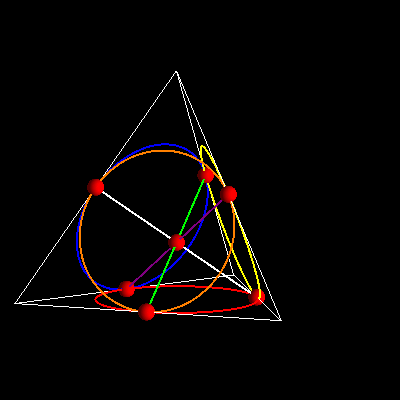
Ilu transformacji symetrii możemy doliczyć się w modelu trójkątnym?
Możemy obrócić nasz trójkąt o 120 stopni, powiedzmy przeciwnie do kierunku ruchu wskazówek zegara. Punkty i linie ulegną przy tym następującej transformacji:
P5 do P1, P1 do P4, P4 do P5, P6 do P2, P2 do P0, P0 do P6
P3 do P3 (nie zmieni miejsca)
l2 do l0, l0 do l3, l3 do l2,l5 do l1,l1 do l4,l4 do l5
l6 do l6 (przejdzie w siebie)
Możemy też obrócić o 240 stopni (przeciwnie do ruchu wskazówek zegara), albo o 120 stopni zgodnie z ruchem wskazówek zegara – na to samo wyjdzie.
Możemy też obrócić o 360 stopni (wszystkie obroty względem środka!), co wyjdzie na to samo jakby niczego nie ruszać – transformacja identycznościowa. Mamy więc trzy różne transformacje. Dla celów buchalteryjnych zawsze liczymy transformację identycznościową. Złożenie (wykonanie jedna po drugiej) dwóch takich obrotów daje obrót trzeci. Mówimy, że mamy grupę o trzech elementach.
Jest jednak i innego rodzaju transformacja, ni dająca się sprowadzić do obrotu: to odbicie względem osi l0 łączącej P0 i P1. Przy takim odbiciu żaden z punktów P0,P1,P3 nie zmienia miejsca. Dwukrotne odbicie (względem tej samej osi) to transformacja identycznościowa. Mamy więc grupę o dwóch elementach.
Obroty (mamy ich trzy) i odbicia (mamy ich dwa) możemy łączyć. Takich połączeń jest 3x2=6. Mamy więc sześć transformacji symetrii w modelu trójkątnym
Czemu nie liczę odbicia względem osi, powiedzmy l2? Bo to już nic nowego. To odbicie możemy uzyskać z połączenia już przez nas zaksięgowanych transformacji. Bowiem najpierw możemy odbić względem l0, potem obrócić o 120 stopni.
W modelu o symetrii siedmiokrotnej liczba symetrii jest oczywista: mamy obrót o 360/7 stopni, który możemy powtarzać 0,1,2,3,4,5,6 razy. Siedem elementów w grupie symetrii. Mamy też odbicie. Podobnie jak dla trójkąta włączamy podwójne odbicie (transformację tożsamościową). Razem widzimy więc 7x2=14 elementów symetrii.
Uwaga:Bjab słusznie zauważył, że to moje rozumowanie jest niepoprawne. Odbicie nie jest symetrią! Złudzenie symetrii wynika jedynie z faktu, że pokolorowałem jedynie dwie linie. Linie nie są symetryczne - nadają "kierunek wirowania". Mamy zatem jedynie siedem oczywistych symetrii, nie zaś 14.
A co z modelem czworościanu foremnego? Tutaj mamy cztery trójkąty. Dla każdego trójkąta mamy grupę sześcioelementową. 4X6=24. Grupa symetrii modelu czworościennego ma zatem, licząc mechanicznie, 24 elementy.
Ile różnych elementów symetrii ma zatem nasza geometria? Kluczowe jest tu słówko „różnych”. Idzie o to, by nie liczyć dwukrotnie. Bo skąd z góry wiadomo, że jedna z symetrii siedmiokrotnych nie jest przypadkiem ta samą transformacją co któryś z obrotów i któreś z odbić modelu trójkątnego lub czworościennego? I skąd wiadomo, że jakiejś symetrii nie przegapiliśmy, bo przecież mogą być jeszcze inne modele?
O tym będzie w kolejnej notce.
Na zakończenie: transformacje symetrii danej geometrii (lub, ogólniej, struktury matematycznej), nazywamy automorfizmami. Pytamy więc: ilu-elementowa jest grupa automorfizmów geometrii Fano.
P.S. Zacząłem budować model czworościenny z kulek magnetycznych:

