Dlaczego trzy wymiary a nie dwa lub dwadzieścia dwa?

Biorąc trzy patyki możemy ustawić je pod katami prostymi. Z czterema już nie wychodzi, a czym patyków więcej – tym gorzej. Długość, szerokość, wysokość – tak podajemy wymiary w katalogach. Graficy komputerowi programujący gry operują współrzędnym x,y,z. Jeszcze trochę a będziemy mieli w kinach trójwymiarowe filmy. Te dwuwymiarowe będą należały do przeszłości tak jak dziś do przeszłości należą filmy czarno-białe. W istocie, tu i ówdzie już dziś widzowie dostają przy wejściu do kina specjalne okulary do widzenia przestrzennego – tzn. trójwymiarowego.

Dlaczego nasz świat wydaje się mieć właśnie trzy wymiary? Co by mu szkodziło mieć cztery lub pięć? A może to nie o świat idzie a o nas? Może to my jesteśmy tak skonstruowani, że ze świata wielowymiarowego konstruujemy trójwymiarową rzeczywistość? Inaczej nie potrafimy. Jednak ta skonstruowana przez nas trójwymiarowa rzeczywistość jest całkiem to a całkiem konsystentna. Więc o coś więcej niż tylko o myślową konstrukcję tu chodzi. Nasz świat ma obiektywnie cechy świata trójwymiarowego. No, tu i ówdzie może wystaje poza trzy wymiary, ale to tylko tu i ówdzie i tylko czasami. Na ogół w trzech wymiarach się świetnie mieścimy i niczego więcej, jak się wydaje, nam nie potrzeba. Dlaczego?

Aktualnie trwa dyskusja na te tematy na Physicsforums. Na przykład w wątkach „Dimensions of Spacetime”i „What made the universe have 3 dimensions, instead of some other number?„. Moi koledzy, matematycy z Warszawy są zainteresowani tym jak wyglądać by mógł odpowiednich równań Maxwell w świecie o liczbie wymiarów różnej od 3. Ja w serii notek dyskutuję kwaterniony, a tych urojonych, odkrytych prze Hamiltona i wydrapanych przez niego scyzorykiem na moście Brougham jest właśnie trzy.

Próbować odpowiedzieć na postawione w tytule pytanie można na wiele sposobów. Trzy jest jednak liczbą a liczbami i strukturami z liczb powstałymi zajmuje się matematyka. Dlatego rzeczą naturalną jest zaprzęgnięcie w pierwszym rzędzie do pracy matematyki. Co ta ma do powiedzenia o wyjątkowości liczby trzy gdy idzie o to ile wymiarów ma przestrzeń?

Odpowiedź uzyskujemy natychmiast: cechą charakterystyczną przestrzeni 3-wymiarowej jest istnienie w niej iloczynu wektorowego dwóch wektorów, iloczyn ten nie tylko daje się w naturalny sposób zdefiniować, lecz także ma szereg bardzo przyjemnych własności. Można o tym poczytać w witrynie fizyka.org lub, więcej i bardziej wyczerpująco, w Wikipedii.

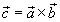
vector product

Jak przypomnieli mi ostatnio koledzy matematycy z Warszawy, operacja iloczynu wektorowego istnieje jedynie w przestrzeniach o trzech i siedmiu wymiarach. W trzech wymiarach związana jest z istnieniem kwaternionów, w siedmiu wymiarach z istnieniem oktonionów. I to już koniec. W żadnej innej liczbie wymiarów nic podobnego skonstruować się, w naturalny a nie sztuczny sposób, nie da. W fizyce iloczyn wektorowy pojawia się gęsto i obficie. Typowe przykłady to siły magnetyczne vxb.png, siła Coriolisa

, ....

Jak zauważył jeden z dyskutantów na Physicsformus, gdyby nie iloczyn wektorowy, to nie moglibyśmy mieć rowerów: „without a cross product (e.g. in 4D or 5D) how will you build a bicycle!„ To jest argument!

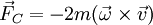No dobrze, ale co z tymi siedmioma wymiarami? Czy nasz świat nie mógłby być siedmiowymiarowy? Niby mógłby, ale nie byłby tak piękny i łatwy dla życia jak ten trójwymiarowy. Bierze się to stąd, że mnożenie kwaternionów choć nie jest przemienne, to jest łączne: (ab)c= a(bc). Możemy więc po prostu napisać abc – nawiasy w mnożeniu można opuścić. Dla oktonionów juz tak nie jest. Świat oktonionów pełen jest nawiasów. Fizyka najwyraźniej za tymi nawiasami nie przepada. Dla kwaternionów możemy napisać abcdef i ma to sens. Dla oktonionów trzeba by sprecyzować co mamy na myśli, np

((a(bc))d)(ef). Obrzydliwość. W dodatku Maxwell wiązał kwaterniony z operacjami. Składanie operacji jest zawsze łączne. Każdy oktonion można traktować jako operację, ale wtedy mnożenie w algebrze oktonionów nie odpowiada składaniu odpowiadających im operacji. Paskudne.

Zostają nam więc trzy wymiary. W siedmiowymiarowym świecie jazda na rowerze byłaby zbyt trudna do opanowania.

Przyjrzyjmy się więc naszym trzem wymiarom dokładniej, pod lupą, a możemy to zrobić gdyż mamy niezłą lupę do dyspozycji. Lupą tą jest algebra Clifforda, którą wprowadziłem w poprzednich w dwóch poprzednich notkach: Maxwell i kwaterniony – Cz. 3, Maxwell i kwaterniony – Cz. 4.

Była to jedna z wielu algebr Clifforda oznaczanych przez Cl(r,s). Dyskutowaliśmy na razie wyłącznie algebrę Cl(0,3). Liczba r to liczba wektorów bazowych o kwadracie równym +1, liczba s to iliczba wektorów bazowych o kwadracie równym -1. W różnych monografiach i publikacjach oznaczenia mogą być nieco inne.

Wybraliśmy tam kwadraty trzech wektorów bazowych równe -1, bo chcieliśmy kwaternionów. Okazało się jednak, że kwaterniony są gdzie indziej, nie w samych wektorach a w ich iloczynach!

Lepszą algebrą Clifforda jest algebra Cl(3,0), gdzie kwadraty wektorów bazowych są równe +1 – zatem równe ich długości. I na taką to algebrę odtąd przejdziemy. Jest o wiele lepsza! Co się zmieni przy takiej strukturze? Niewiele.

Oznaczmy naszą 3-wymiarową przestrzeń literą V. Dlaczego V? Tak się przyjęło. W angielskim „wector” pisze się „vector”, no to przestrzeń wektorów oznacza się często właśnie literką V. Zbiór liczb rzeczywistych (skalarów) oznaczmy literką R. Nasza algebra Clifford rozpinana jest wtedy przez jednowymiarowe R, trójwymiarowe V, trójwymiarową przestrzeń dwuwektorów, i jednowymiarową przestrzeń trójwektorów. Dobrze jest mieć jakiś zapis na przestrzeń dwuwektorów i na przestrzeń trójwektorów. Użyjemy symbolu V∧ V dla przestrzeni dwuwektorów i V∧V∧V dla przestrzeni trójwektorów. Zatem

R – skalary (1 wym)

V - wektory (3 wym)

V∧V – dwuwektory (3 wym)

V∧V∧V – trójwektory (1 wym)

Każdy skalar jest proporcjonalny do liczby 1.

Każdy wektor r w naszej algebrze jest kombinacją trzech wektorów bazowych:

r = x e₁+ y e₂+ ze₃

Każdy dwuwektor jest kombinacją trzech bazowych dwuwektorów:

e(n) = n_x e₂₃+ n_y e₃₁+ n_z e₁₂

Każdy trójwektor jest proporcjonalny do trójwektora e = e₁e₂e₃. Kto nie przeczytał notki Maxwell i kwaterniony – Cz. 3, a także następnej – będzie miał problemy ze zrozumieniem – tak to już jest i nie ma na to rady. To znaczy mała rada jest. To przypomnienie, że nasza algebra Clifforda opiera się na wyjściowych regułach mnożenia , które teraz wyliczę modyfikując znaki:

e₁e₂ = -e₂e₁

e₂e₃ = -e₃e₂

e₃e₁ = -e₁e₃

e₁²= e₂²= e₃²= 1

a także, że wprowadziliśmy oznaczenia:

e₁₂ = e₁e₂

e₂₃ = e₂e₃

e₃₁ = e₃e₁

e = e₁e₂e₃

Skalary i dwuwektory rozpinają same algebrę – nazywamy ją podalgebrą parzystą. Wektory i trójwektory rozpinają część nieparzystą algebry. Podczas gdy iloczyn dwóch elementów parzystych algebry jest dalej elementem parzystym, to iloczyn dwóch elementów nieparzystych nie jest elementem nieparzystym, przeciwnie, jest elementem parzystym. Można się o tym łatwo przekonać bawiąc się mnożeniem z użyciem naszych reguł.

Gdzie się teraz ukrywają kwaterniony? Łatwo się przekonać, że jeśli teraz zdefiniujemy:

i = -e₂₃

j= -e₃₁

k = -e₁₂

to reguły mnożenia kwaternionów są spełnione (sprawdź to!).

Zmienia się też kwadrat trójwektora e:

e² =e₁e₂e₃e₁e₂e₃=...=-1. (sprawdź to!)

Nasz bazowy trójwektor ma więc teraz własność urojonego i. W naszej algebrze Clifforda Cl(3,0) mamy więc teraz zarówno kwaterniony – rozpięte przez (1,i,j,k) jak i liczby zespolone, rozpięte przez (1,e). W dodatku, jak łatwo sprawdzić, nasze liczby zespolone są przemienne z kwaternionami (sprawdź to!). Jedne i drugie są przydatne w fizyce i w technice. Nasza algebra Cl(3,0) ma więc zachęcającą i bogatą strukturę.

Przyjrzyjmy się teraz iloczynowi (policzonemu w algebrze) dwóch wektorów, wektora

a = a_x e₁ + a_y e₂ + a_z e₃

i wektora

b = b_x e₁ + b_y e₂ + b_z e₃

Wektory należą do części nieparzystej algebry, ich iloczyn będzie zatem należał do podalgebry parzystej. Będzie zatem miał część skalarną i część dwuwektorową. Wymnażając z uzyciem naszych reguł mnożenia z łatwością otrzymamy wynik, który można uporządkować tak (sprawdź to!):

ab = (a_xb_x+a_yb_y+a_zb_z) + (a_yb_z-a_zb_y)e₂₃+(a_zb_x-a_xb_z)e₃₁+(a_xb_y-a_yb_x)e₁₂

Człon pierwszy, w nawiasie, jest skalarem. W istocie rozpoznajemy w nim iloczyn skalarny a.b wektorów a i b. (Zwróćmy uwagę na kropkę pomiędzy a i b) Reszta jest dwuwektorem. Współczynniki liczbowe przy dwuwektorach bazowych rozpoznajemy jako składowe iloczynu wektorowego axb. Zapisujemy to jako:

ab = a.b + a∧b

Iloczyn skalarny jest symetryczny:

a.b = b.a

Ten drugi człon nazywamy iloczynem zewnętrznym. Jest on antysymetryczny:

a∧b = - b∧a

Sam iloczyn ab = nie jest na ogół ani symetryczny ani antysymetryczny. Nazywamy go czasem iloczynem geometrycznym, a samą algebrę – algebrą geometryczną.

Nietrudno sie przekonać, że (sprawdź to!)

a.b = ½ (ab+ba)

a∧b = ½ (ab-ba)

Struktura ta byłaby dla Maxwella skarbem – gdyby ją był znał! Zobaczymy wkrótce jak mieszczą się w niej i jak działają Maxwellowskie „rotory” dla których prof. Bernard Jancewicz proponuje inna nazwę - „volutors”, bowiem po Łacinie „volutare” to „toczyć się”. No, nie wiem, ja tam nie widzę by się coś toczyło, widzę natomiast, że się coś obraca. Tak czy siak istnieją prace w których zaproponowana przez Jancewicza nazwa została użyta. Oto jedna z nich: Valeri V. Dvoeglazov, „Lagrangian Formulation of the Joos-Weinberg's 2(2S+1)-- theory and Its Connection with the Skew-Symmetric Tensor Description”.

Podumowanie: Wprowadziliśmy algebrę Clifforda Cl(3,0) – podstawową strukturę algebraiczną kodującą geometrię naszego trójwymiarowego świata. Zobaczyliśmy, że iloczyn w tej algebrze zawiera dwie podstawowe operacje na wektorach: iloczyn skalarny i iloczyn wektorowy. Cała mechanika klasyczna opiera się na tych dwóch operacjach. Iloczyn skalarny potrzebny jest przy obliczaniu pracy wykonywanej przez siłę działającą pod jakimś kątem do trajektorii. Kto o tym nie wie, ten będzie uparcie twierdził, że Ziemia się męczy utrzymując Księżyc na orbicie. Iloczyn wektorowy pojawia się w mechanice ciał wirujących – a tych jest wiele, na przykład w wielu silnikach, także w rowerach. Jeden i drugi są u podstaw sformułowania praw elektromagnetyzmu – bez którego życie na Ziemi nie mogłoby istnieć w swej cielesnej postaci. W następnej notce zajmiemy się obrotami bliżej.